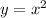 - это парабола, с вершиной в точке (0;0). Она симметрична относительно оси OY. Ветви направлены вверх. Проходит через точки (0;0), (2;4), (-2;4)
- это парабола, с вершиной в точке (0;0). Она симметрична относительно оси OY. Ветви направлены вверх. Проходит через точки (0;0), (2;4), (-2;4)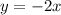 - это прямая, для её построения достаточно 2х точек. Например (0;0) и (-2;4)
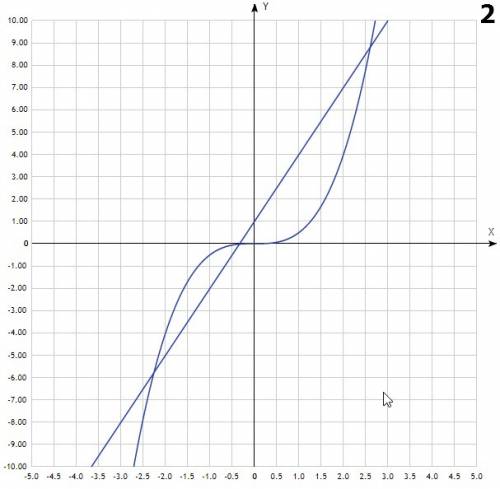
- это прямая, для её построения достаточно 2х точек. Например (0;0) и (-2;4)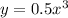 - кубическая парабола. График симметричен относительно начала координат, т.е. точки (0;0).
- кубическая парабола. График симметричен относительно начала координат, т.е. точки (0;0). 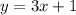 - прямая, проходящая через точки (0;1), (1;4)
- прямая, проходящая через точки (0;1), (1;4) - прямая, проходящая через точки (0;-2) и (1;0)
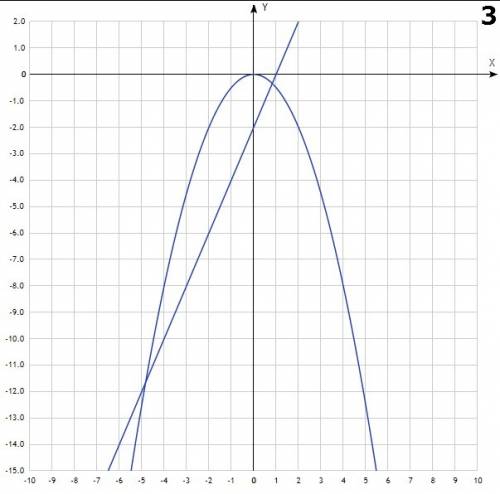
- прямая, проходящая через точки (0;-2) и (1;0) - парабола, с вершиной в точке (0;0), симметричная относительно OY. Ветви направлены вниз.
- парабола, с вершиной в точке (0;0), симметричная относительно OY. Ветви направлены вниз. 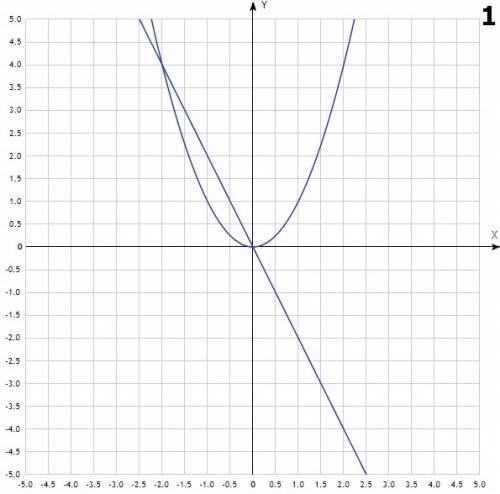
cos t = p / √3
cos 2t = 2cos²t - 1 = 2·p²/3 - 1
sin (π/3 + t) · sin (π/3 - t) = 1/2 (cos 2t - cos (2π/3)) = 1/2 · cos 2t - 1/2 · (-1/2) =
= 1/2 cos 2t + 1/4 = 1/2 · (2·p²/3 - 1) + 1/4 = p²/3 - 3/4