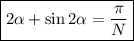Алгебра: Какое из чисел заключено между 5/7 и 9/11 1) 0,6 2) 0,7 3) 0,8 4) 0,9

Какое из чисел заключено между 5/7 и 9/11 1) 0,6 2) 0,7 3) 0,8 4) 0,9

👇

Увидеть ответ

Ответ:

yaannase

30.04.2020

Первый вариант ответа 0,6.

4,5(40 оценок)

Открыть все ответы

Ответ:

Yuliaddd

30.04.2020

1) Линейной функцией называется функция вида y = kx + b,

где k – угловой , b – свободный член , x – независимая переменная.

Примеры линейных функций:

у = 3х ,

у = х +2

у = 6х - 5

у = х,

у = - 1/2 х +10

у = - 0,3 х - 1

Графиком линейной функции является прямая.

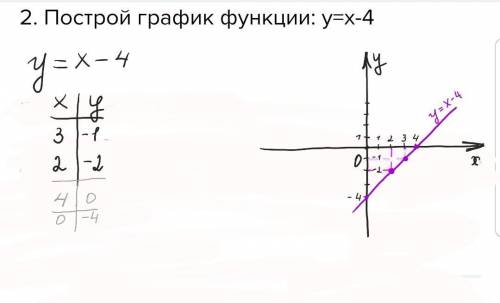
2) у=х-4

Это линейная функция. Графиком данной функции является прямая.

Для построение прямой необходимо найти две точки.Находим:

если х= 3, то у= 3-4 = -1

если х= 2, то у = 2-4 = -2 (лучше найти три точки ,третью для проверки: х= 0,у= -4 ).

Отмечаем точки на графике,соединяем,строим график.

Алгебра. 1.Какая функция называется линейной функцией? Приведн примеры линейных функции2. Построй гр

4,7(61 оценок)

Ответ:

tim228904

30.04.2020

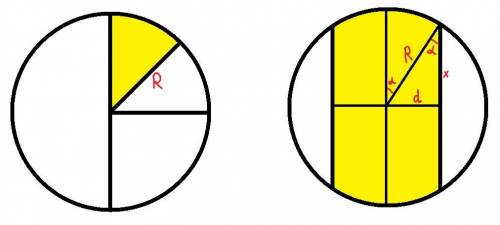
Так как тортики имеют постоянную высоту, то вместо рассмотрения объемов буем рассматривать соответствующие площади оснований.

Площадь основания тортика радиуса R:

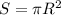
$S=\pi R^2$

Тогда, площадь основания одного Машиного куска:

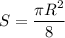
$S=\dfrac{\pi R^2}{8}$

Рассмотрим Дашин кусок (на картинке). Вертикальной и горизонтальной прямой разобьем его на 4 равные части и рассмотрим одну из них. Проведем еще одну прямую так, чтобы эта часть разделилась на сектор и прямоугольные треугольник.

Рассмотрим полученный сектор. Пусть α - угол между радиусами, образующими сектор. Тогда, площадь сектора:

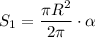
$S_1=\dfrac{\pi R^2}{2\pi} \cdot \alpha$

Рассмотрим прямоугольный треугольник. Зная, что накрест лежащие углы при параллельных прямых равны, получим, что один из острых углов этого треугольника равен α. Выразим через этот угол и известный радиус катеты треугольника:

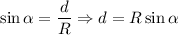
$\sin \alpha=\dfrac{d}{R} \Rightarrow d=R\sin \alpha$

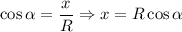
$\cos \alpha=\dfrac{x}{R} \Rightarrow x=R\cos \alpha$

Площадь прямоугольного треугольника:

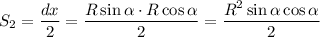
$S_2=\dfrac{dx}{2} =\dfrac{R\sin \alpha \cdot R\cos\alpha }{2} =\dfrac{R^2\sin \alpha \cos\alpha }{2}$

Тогда, запишем сумму, представляющую площадь основания четверти кусочка Даши:

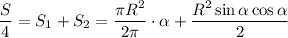
$\dfrac{S}{4}=S_1+S_2=\dfrac{\pi R^2}{2\pi} \cdot \alpha+\dfrac{R^2\sin \alpha \cos\alpha }{2}$

Отсюда площадь основания кусочка Даши:

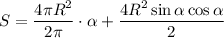
$S=\dfrac{4\pi R^2}{2\pi} \cdot \alpha+\dfrac{4R^2\sin \alpha \cos\alpha }{2}$

По условию куски Маши и Даши должны быть одинаковы. значит:

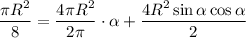
$\dfrac{\pi R^2}{8}=\dfrac{4\pi R^2}{2\pi} \cdot \alpha+\dfrac{4R^2\sin \alpha \cos\alpha }{2}$

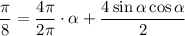
$\dfrac{\pi}{8}=\dfrac{4\pi}{2\pi} \cdot \alpha+\dfrac{4\sin \alpha \cos\alpha }{2}$

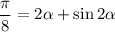
$\dfrac{\pi}{8}=2\alpha+\sin2\alpha$

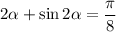
$2\alpha+\sin2\alpha=\dfrac{\pi}{8}$

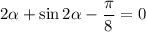
$2\alpha+\sin2\alpha-\dfrac{\pi}{8}=0$

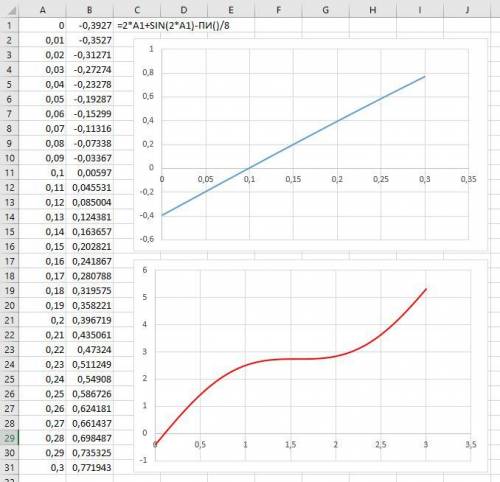
Для решения уравнения построим график в Microsoft Excel (картинка).

По графику определим, что равенство выполняется при 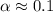$\alpha \approx 0.1$ .

График при $x\to0$ напоминает прямую, так как в данном случае имеем место быть первый замечательный предел.

Действительно, можно считать, что рассматриваемый угол α мал. Тогда: 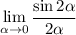$\lim\limits_{\alpha \to0}\dfrac{\sin2\alpha }{2\alpha }$ в соответствии с первым замечательным пределом. Тогда от имеющегося уравнения можно перейти к более простому:

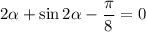
$2\alpha+\sin2\alpha-\dfrac{\pi}{8}=0$

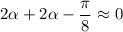
$2\alpha+2\alpha-\dfrac{\pi}{8}\approx0$

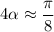
$4\alpha\approx\dfrac{\pi}{8}$

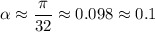
$\alpha\approx\dfrac{\pi}{32}\approx0.098\approx0.1$

Искомое расстояние от оси симметрии соответствует уже вводившейся величине d:

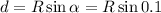
$d=R\sin \alpha=R\sin 0.1$

По той же причине синус малого аргумента можно заменить самим этим аргументом. Получим:

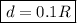
$\boxed{d=0.1R}$

В частности, для практических целей выполненные приближенные допущения вполне допустимы и удачны.

Вернемся к полученному ранее уравнению:

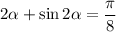
$2\alpha+\sin2\alpha=\dfrac{\pi}{8}$

Заметим, что информация о том, что Маша разрезала свой тортик на 8 частей, сосредоточена в знаменателе правой части. Поэтому, если изначально Маша разрезала тортик на N частей, то проведя аналогичные рассуждения мы получим уравнение вида:

$\boxed{2\alpha+\sin2\alpha=\dfrac{\pi}{N}}$