Для того чтобы разложить на множители выражение вида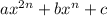 
, где 
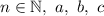— числа, достаточно решить квадратное уравнение 
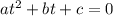, где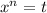 
, и применить формулу разложения: 
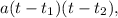где 
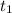и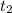 
— корни данного квадратного уравнения, после чего нужно сделать обратную замену.
Итак, имеем биквадратный трехчлен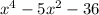 
. Сделаем подходящую замену: 
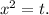Получили квадратный трехчлен 
.
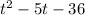Решим уравнение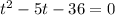 
при теоремы Виета:
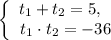
Получили корни: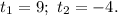 
Подставим полученные корни в формулу: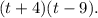 
Сделаем обратную замену: 
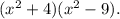Применим формулу разности квадратов 
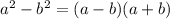и получаем окончательное разложение данного биквадратного трехчлена: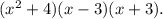 
Воспользуемся методом группирования (группировки):
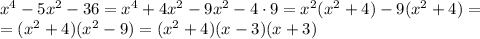
ответ: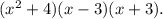
a ∈ (-oo; -1) U {0} U (1; +oo)
Объяснение:
1) При x < 1 будет |x - 1| = 1 - x
1 - x = ax
1 = ax + x
x = 1/(a+1) < 1
При a = -1 корней нет. При всех других а проверяем неравенство
1/(a+1) - 1 < 0
(1-a-1)/(a+1) < 0
-a/(a+1) < 0
a/(a+1) > 0
a ∈ (-oo; -1) U (0; +oo)
2) При x = 1 будет
|1 - 1| = a*1
a = 0
Подходит, потому что корень только один: x = 1
3) При x > 1 будет |x - 1| = x - 1
x - 1 = ax
x - ax = 1
x = 1/(1-a)
При а = 1 корней нет.
При всех других а проверяем неравенство
1/(1-a) - 1 > 0
(1-1+a)/(1-a) > 0
a/(1-a) > 0
a/(a-1) < 0
a ∈ (0; 1)
Получаем a1 ∈ (-oo; -1) U (0; +oo); a2 ∈ (0; 1)
Промежуток а2 вырезается из промежутков а1.
ответ: a ∈ (-oo; -1) U {0} U (1; +oo)
1080 * 1/3 = 360 мл. молока для 1080 мл. кофе.