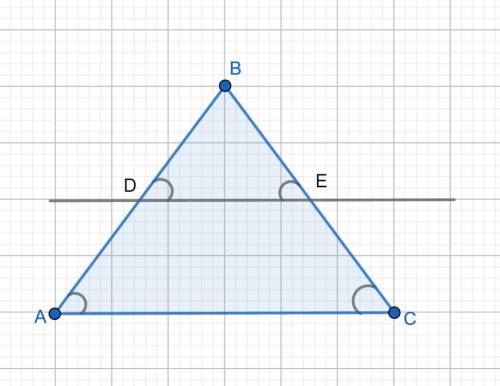
Можно доказать несколькими По т. Фалеса: Если параллельные прямые отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на второй стороне угла.
Параллельные прямые DE и AC отсекают равные отрезки на стороне AB угла ABC, т.е. AD = DB. Значит на стороне BC они отсекают также равные отрезки BE = EC.
2) Из подобия треугольников. Так как DE ║ AC, то ΔABC подобен ΔDBE по двум углам: ∠B общий, ∠BDE = ∠BAC как соответствующие при DE ║ AC и секущей AB. Так как по условию AD = DB, то BD/AB = 1/2. Коэффициент подобия k = 1/2. ⇒ BE/BC = 1/2, ⇒ BC = 2*BE, тч. E является серединой отрезка ВС.
3) Проведем прямые BO ║AC и ON║AB.
DBON параллелограмм, так как его противолежащие стороны параллельны. ⇒ DB = EO. ADEN параллелограмм, так как его противолежащие стороны параллельны, так как AD=DB, то NE=EO.
ΔBEO = ΔNEC по второму признаку: ∠BEO = NEC вертикальные, ∠BOE = ∠ENC внутренние накрест лежащие при BO ║AC и секущей ON. OE = EN. Из равенства треугольников следует BE=EC. ( так доказывается т. Фалеса)
Можно доказать несколькими По т. Фалеса: Если параллельные прямые отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на второй стороне угла.
Параллельные прямые DE и AC отсекают равные отрезки на стороне AB угла ABC, т.е. AD = DB. Значит на стороне BC они отсекают также равные отрезки BE = EC.
2) Из подобия треугольников. Так как DE ║ AC, то ΔABC подобен ΔDBE по двум углам: ∠B общий, ∠BDE = ∠BAC как соответствующие при DE ║ AC и секущей AB. Так как по условию AD = DB, то BD/AB = 1/2. Коэффициент подобия k = 1/2. ⇒ BE/BC = 1/2, ⇒ BC = 2*BE, тч. E является серединой отрезка ВС.
3) Проведем прямые BO ║AC и ON║AB.
DBON параллелограмм, так как его противолежащие стороны параллельны. ⇒ DB = EO. ADEN параллелограмм, так как его противолежащие стороны параллельны, так как AD=DB, то NE=EO.
ΔBEO = ΔNEC по второму признаку: ∠BEO = NEC вертикальные, ∠BOE = ∠ENC внутренние накрест лежащие при BO ║AC и секущей ON. OE = EN. Из равенства треугольников следует BE=EC. ( так доказывается т. Фалеса)

1) x(a-b)+y(b-a);
2)m²(a-2)+n(2-a).
* * * * * * * * * *
1)
x(a-b)+y(b-a) = x(a-b)-y(a -b) =(a-b)(x-y).
2)
m²(a-2)+n(2-a) = m²(a-2) - n(a -2) =(a -2)(m² -n).
Если (допустим):
2) m²(a-2)+n²(2-a) = m²(a-2) - n²( a -2) = ( a -2)(m² - n²) =( a -2)(m - n)(m+n) .