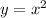- это парабола, с вершиной в точке (0;0). Она симметрична относительно оси OY. Ветви направлены вверх. Проходит через точки (0;0), (2;4), (-2;4)
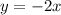- это прямая, для её построения достаточно 2х точек. Например (0;0) и (-2;4)
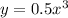- кубическая парабола. График симметричен относительно начала координат, т.е. точки (0;0). 
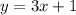- прямая, проходящая через точки (0;1), (1;4)
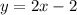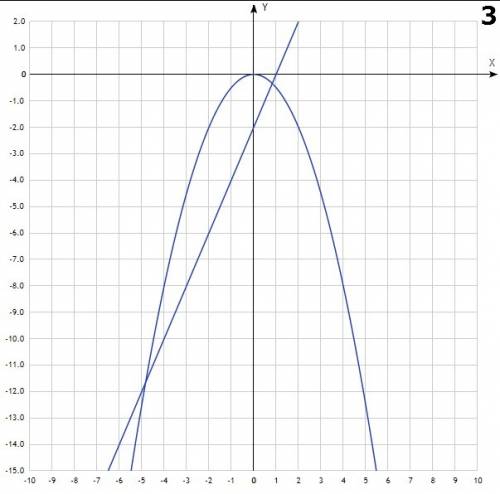
- прямая, проходящая через точки (0;-2) и (1;0)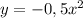
- парабола, с вершиной в точке (0;0), симметричная относительно OY. Ветви направлены вниз. 
ОДЗ
{x-3≥0⇒x≥3
{x-7≥0⇒x≥7
{x+3≥0⇒x≥-3
x∈[7;∞)
возведем в квадрат
(x-3)(x-7)=x+3
x²-7x-3x+21-x-3=0
x²-11x+18=0
x1+x2=11 U x1*x2=18
x1=2∉ОДЗ
х=9
2
ОДЗ
{x-4>0⇒x>4
{x+6>0⇒x>-6
x∈(4;∞)
lg[(x-4)(x+6)]=lg8
(x-4)(x+6)=8
x²+6x-4x-24-8=0
x²+2x-32=0
D=4+128=132
x1=(-2-2√33)/2=1-√33∉ОДЗ
x2=1+√33
3
ОДЗ
{x+3>0⇒x>-3
{x+6>0⇒x>-6
x∈(-3;∞)
log(2)(√(x+3)(x+6))=1
√(x²+9x+18)=2
x²+9x+18=4
x²+9x+14=0
x1+x2=-9 U x1*x2=14
x1=-7∉ОДЗ
х=-2