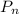=n! = 1·2·3·4 = 24 - варианта
Объяснение:
Задано число:
52*2*
Заметим, что
36 = 4*9, то есть число должно делиться и на 4, и на 9.
1)
Признак делимости на 4:
Число делится на 4, если его запись оканчивается двумя цифрами, образующими число, которое делится на 4 или его запись оканчивается двумя нулями.
Поскольку предпоследняя цифра не равна нулю, то остаются кандидаты:
20; 24 и 28.
2)
Признак делимости на 9:
Число делится на 9, если сумма цифр целого числа делится на 9.
Заметим, что сумма трех цифр нашего числа уже делится на 9:
5+2+2=9 - делится на девять.
Рассмотрим три последние цифры.
*2*
Заметим, что последняя цифра - четная (число должно делиться на 4).
Возможные комбинации:
020 (0+0=0)
128 (1+8=9)
326 (число 26 не делится на 4)
524 (5+4=9)
722 (число 22 не делится на 4)
920 (9+0=9)
Осталось 4 числа:
52020
52128
52524
52920
Это задача на размещение без повторений, т.е. при данном размещении 1 человек не может в одной и той же комбинации занять 2 места сразу.
(То, что Вы написали P₄=4! - в размещении используется только тогда, когда число размещений равно числу объектов - формула А₄⁴=P₄=4!), фоа здесь используем формулу размещения:
А³₄=4!/(4-3)!=4!/1!=4*3*2=24
4*3*2 - означает, что в каждой комбинации 1-ый человек может выбрать любое из 4-х мест,
2-ой - любое из 3-х оставшихся,
3-й - любое из 2-х оставшихся