x₁ = 2 + 
, y₁ = 2 - 3;
x₂ = 2 -, y₂ = - 3 - 2:
Объяснение:
{ху - х = 4
{2х - у = 7
Выразим y и подставим во второе уравнение
{xy - x = 4
{-y = 7 - 2x
Уберём минус перед y, помножив выражение на (-1)
{xy - x = 4
{y = 2x - 7
Подставляем полученное выражение вместо y
x * (2x - 7) - x = 4
2x² - 7x - x =4
2x² - 8x - 4 = 0
Получаем квадратное уравнение. Сокращаем коэффиценты, деля обе стороны на 2
x² - 4x - 2 = 0
У нас a = 0. По теореме Виета: x₁ + x₂ = −b; x₁ * x₂ = c;
Но для начала проверим дискриминант
D = b² - 4ac
D = 16 - 4 * 1 * (-2)
D = 16 + 8 = 24
Нет такого натурального числа, которое было бы квадратным корнем из 24, поэтому мы не сможем решить теоремой Виета, и продолжаем решать дискриминантом
x₁,₂ = 
x₁ = 
= 
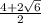= 2 +
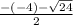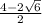x₂ = 
= 
= 2 -
Находим y, подставляя x
2 * (2 + ) - y₁ = 7
4 + 2 - y₁ = 7
- y₁ = 3 - 2
Убираем минус
y₁ = 2 - 3
Ищем y₂
2 * (2 - ) - y₂ = 7
4 - 2 - y₂ = 7
- y₂ = 3 + 2
Снова убираем минус
y₂ = - 3 - 2
ответ: x₁ = 2 + , y₁ = 2 - 3; x₂ = 2 -, y₂ = - 3 - 2;
а). В этом числе ноль встречается 9 раз, а числа 2, 3, 9 - по 20 раз.
б). Да, 123...9899 делится на 9.
Сначала посчитаем, сколько всего в числе 1234..9899 было выписано цифр 0, 1, 2, 3, 9. Это тоже самое, что и посчитать, сколько раз встречаются эти же цифры в числах от 1 до 99.
Цифра 0:
10, 20, 30, 40, 50, 60, 70, 80, 90 - всего 9 раз.
Цифра 1:
1, 10 - 19 (11 раз), 21, 31, 41, 51, 61, 71, 81 ,91 - всего 20 раз.
Понятно, что 2, 3, 9 встречаются столько же раз, сколько и 1 (все они могут стоять 10 раз в разряде единиц, и 10 раз - в разряде десятков).
Теперь нужно узнать, делится ли число 1234..9899 на 9.
Признак делимости на 9: число делится на 9 тогда и только тогда, когда сумма его цифр тоже делится на 9.Так что мы должны узнать, делится ли 1 + 2 + 3 + ... + 99 на 9.
Для этого найдем искомую сумму по формуле арифметической прогрессии:
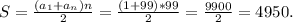
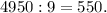
Так как получилось разделить нацело, то 1234...9899 делится на 9.
t=arctg(-1/4)
tgt=-1/4; 1+tg^2 t=1/cos^2 t
1+(-1/4)^2=1/cos^2 t; 1+1/16=(16+1)/16=17/16
1/cos^2 t=17/16; cos^2 t=16/17
sin^2 t+cos^2 t=1; sin^2 t=1-cos^2 t; sin^2 t=
=1-16/17=1/17