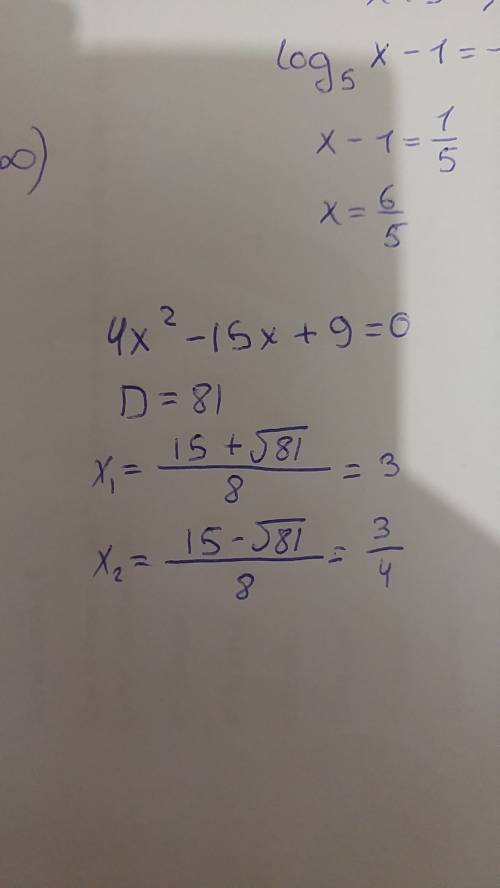
Так как сумма чисел в вершинах есть нечетное число, то как минимум одно число в вершине - нечетное. Получить нечетное число можно лишь перемножая нечетные числа.
Пусть в вершине В нечетное число, тогда на сторонах АВ и ВС нечетные числа.
Чтобы общая сумма чисел в вершинах была нечетной, необходимо оставшиеся три числа взять четными или одно взять четным, а два других нечетными. Но если предположить, что еще хотя бы одно число в вершине нечетное, то по цепочке получим и на следующей стороне нечетное число и после следующего предположения, что в следующей вершине нечетное число (ведь нам нужно два нечетных числа в сумму), на последней стороне получим тоже нечетное число, что будет означать, что и в последней вершине нечетное число. Тогда сумма чисел в вершинах будет четная. Противоречие.
Значит, среди чисел в вершинах только одно нечетное.
По этой расстановке однозначно расставляются числа на сторонах: на двух смежных сторонах - нечетные числа, на двух других смежных сторонах - четные числа.
Проверим наименьший вариант: 1, 1, 2, 2:
1·1+1·2+2·2+2·1=1+2+4+2=9
Возьмем вместо одного из чисел следующее за ним по четности, например вместо 1 возьмем 3:
3·1+1·2+2·2+2·3=3+2+4+6=15
сумма чисел на сторонах 3+1+2+2=8
Можно было взять, например, 4 вместо 2:
1·1+1·2+2·4+4·1=1+2+8+4=15
По-прежнему, сумма чисел на сторонах 1+1+2+4=8
Если числа продолжить как-либо увеличивать, то слагаемые в произведении увеличатся, а соответственно и произведение увеличится и не будет равно 15.
ответ: 8
Объяснение:
1.
(4x+2)/(1+2x)=x-6, где 1+2х≠0; х≠-1/2; х≠-0,5
4x+2=(x-6)(1+2x)
4x+2=x+2x^2 -6-12x
2x^2 -11x-6-4x-2=0
2x^2 -15x-8=0; D=225+64=289
x1=(15-17)/4=-2/4=-0,5 - этот корень не подходит, смотри выше.
x2=(15+17)/4=32/4=8
ответ: 8.
2.
4x^2 -9=0
(2x-3)(2x+3)=0
2x-3=0; x1=3/2=1,5
2x+3=0; x2=-3/2=-1,5
ответ: -1,5 и 1,5.
3x^2 +6=0
3(x^2 +2)=0
x^2 +2=0; x^2=-2 - уравнение не имеет решений, так как квадратный корень не может быть отрицательным.
2x^2 -11x+12=0; D=121-96=25
x1=(11-5)/4=6/4=1,5
x2=(11+5)/4=16/4=4
ответ: 1,5 и 4.
25=26x-x^2
x^2 -26x+25=0
x1+x2=26; 1+25=26
x1•x2=25; 1•25=25
x1=1; x2=25
ответ: 1 и 25.
-x(x+7)=(x-2)(x+2)
-x^2 -7x=x^2 -4
x^2 +7x-4+x^2=0
2x^2 +7x-4=0; D=49+32=81
x1=(-7-9)/4=-16/4=-4
x2=(-7+9)/4=2/4=0,5
ответ: -4 и 0,5.