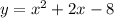
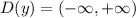
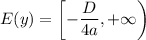 - где D дискриминант.
- где D дискриминант.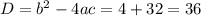
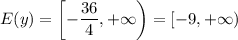
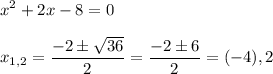



![(-\infty,-1]](/tpl/images/0467/5865/91666.png)

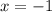
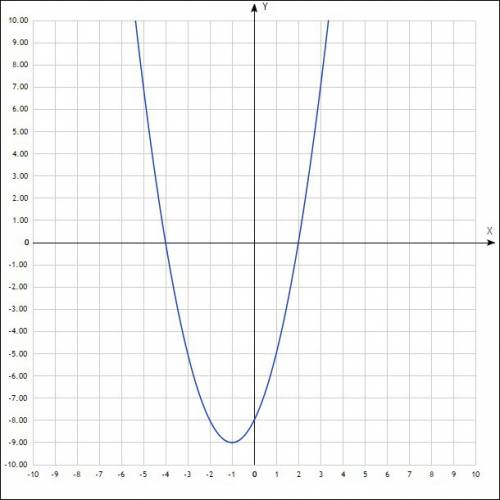
Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t)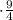 - объем работы системы из двух насосов за 2ч 15мин.
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение: 
9t = 1

Значит, 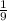 - цис./ч - производительность "медленного" насоса.
- цис./ч - производительность "медленного" насоса.
Тогда 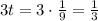 - цис./ч - производительность "быстрого" насоса.
- цис./ч - производительность "быстрого" насоса.
Следовательно, 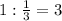 ч - потребуется "быстрому" насосу на заполнение цистерны.
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.

3sin²x/cos²x=2sinx*cosx/cos²x+cos²x/cos²x
3tg²x=2tgx+1
3tg²x-2tgx-1=0
замена переменных: tgx=y
3y²-2y-1=0
D=(-2)²-4*3*(-1)=16
y₁=(-(-2)-4)/(2*3), y₁=-1/3
y₂=(2+4)/6 y₂=1
обратная замена:
y₁=-1/3, tgx=-1/3. x₁=arctg(-1)3+πn, n∈Z
y₂=1, tgx=1. x₂=π/4+πn, n∈Z