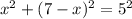 .
.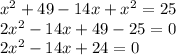 |:2
|:2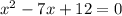
Выделим полный квадрат.
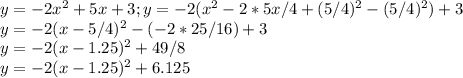
Найдём нули этой функции.
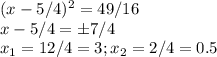
Найдём точку пересечения с осью Оу.
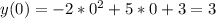
Как я буду строить: я буду последовательно изменять функции
1. Есть функция 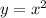 как она выглядит известно.
как она выглядит известно.
2. Функция 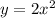 чуть уже, она сжата к оси Оу.
чуть уже, она сжата к оси Оу.
3. 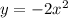 перевёрнута вниз (развернули на 180°).
перевёрнута вниз (развернули на 180°).
4.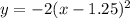 график сдвинут вправо на 1.25.
график сдвинут вправо на 1.25.
5.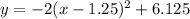 график подняли вверх на 6.125.
график подняли вверх на 6.125.
Получили график нашей функции.
Точки пересечения с осями мы уже знаем, и исходя из переноса функции, можно понять какой будет координата вершины параболы.
Конечно обычно сразу отмечают координаты вершины и соединяют её с нулями функции, просто хотел объяснить по какому принципу строятся функции 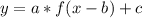 когда известно как выглядит y=f(x).
когда известно как выглядит y=f(x).

№1
Умножим первое ур-ние на 3, получим такую систему ур-ний
9х+3ау=36
9х-15у=36
вычтем второе из первого, получим
3ау+15у=0
или
3(а+5)у=0 делим на 3
(а+5)у=0
только два варианта решений:
1) а+5=0 а=-5 0*у=0 => у-любое - бесконечно множество решений
и х- тоже любое - тоже бесконечно множество решений
или
2) а+5≠0 у=0/(а+5) => у=0 - единственное решение
и х=4 - тоже единственное решение
значит, система всегда имеет решения (или одно или бесконечно много )
ответ: Г ) таких значений а не существует, при которых система не имеет решений - решения есть при любых а - или одно или бесконечно много
№2
2х-7у=6
8х-28у=24
разделим второе на 4, получим
2х-7у=6
2х-7у=6
получили фактически только одно единственное уравнение с двумя неизвестными
2х-7у=6
значения, например, у можно взять любое, тогда х вычисляется из уравнения
2х=6+7у
х=3+(7/2)у
ответ: Г ) у системы бесконечно много решений
Сумма катетов в образованном треугольнике будет равна половина периметру прямоугольника.
Пусть а и б - катеты, с - гипотенуза, один катет = х
По т. Пифагора:
а в квадрате+ б в квадрате = с в квадрате, т. е
х2+(7-х) 2=25
После упрощения:
х2-7х+12=0
По Виету: х1 =4 х2=3
ответ: катеты равны 3 и 4 см