Дана функция у = (х-1)²/x².
1.Область определения функции. D ∈ R : x ≈ 0.
2. Нули функции. Точки пересечения графика функции с осью ОХ.
График функции пересекает ось X при f = 0.
Значит, надо решить уравнение (х-1)²/x² = 0.
Решаем это уравнение (достаточно приравнять нулю числитель):
(х-1)² = 0, х-1 = 0, х = 1.
Точки пересечения с осью X: (1; 0).
График пересекает ось Y, когда x равняется 0.
Подставляем x = 0 в (x - 1)²/x².
Результат: (0 - 1)²/0² невыполним, значит, график не пересекает ось Оу.
3. Промежутки знакопостоянства функции.
Так как переменная в числителе и знаменателе в квадрате, то функция на всей числовой оси только положительна.
4. Симметрия графика (чётность или нечётность функции).
f(-x) = ((-x) - 1)²/((-x)²) = (x + 1)²/x² ≠ f(x) ≠ -f(-x).
Поэтому функция не чётная и не нечётная.
5. Периодичность графика. Не периодична.
6.Точки разрыва, поведение функции в окрестностях точек разрыва, вертикальные асимптоты - смотри приложение.
7. Интервалы монотонности функции, точки экстремумов, значения функции в точках экстремумов.
Первая производная: y' = (1/x²)*(2x - 2) - (2/x³)*(x - 1)²
или y' = (2x - 2)/x³.
Находим нули функции. Для этого приравниваем производную к нулю
(достаточно числитель): 2x-2 = 0
Откуда: x1 = 2/2 = 1.
(-∞ ;0) (0; 1) (1; +∞)
f'(x) > 0 f'(x) < 0 f'(x) > 0
функция возрастает функция убывает функция возрастает.
В окрестности точки x = 1 производная функции меняет знак с (-) на (+). Следовательно, точка x = 1 - точка минимума.
8. Интервалы выпуклости, точки перегиба.
Найдем точки перегибов, для этого надо решить уравнение
\frac{d^{2}}{d x^{2}} f{\left (x \right )} = 0.
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
\frac{d^{2}}{d x^{2}} f{\left (x \right )} =
Вторая производная
\frac{1}{x^{2}} \left(2 - \frac{1}{x} \left(8 x - 8\right) + \frac{6}{x^{2}} \left(x - 1\right)^{2}\right) = 0
Решаем это уравнение
Корни этого ур-ния
x_{1} = \frac{3}{2}
Также нужно подсчитать пределы y'' для аргументов, стремящихся к точкам неопределённости функции:
Точки, где есть неопределённость:
x_{1} = 0.
\lim_{x \to 0^-}\left(\frac{1}{x^{2}} \left(2 - \frac{1}{x} \left(8 x - 8\right) + \frac{6}{x^{2}} \left(x - 1\right)^{2}\right)\right) = \infty.
\lim_{x \to 0^+}\left(\frac{1}{x^{2}} \left(2 - \frac{1}{x} \left(8 x - 8\right) + \frac{6}{x^{2}} \left(x - 1\right)^{2}\right)\right) = \infty.
- пределы равны, значит, пропускаем соответствующую точку.
Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках
(-oo, 3/2]
Выпуклая на промежутках
[3/2, oo)
9. Поведение функции в бесконечности. Наклонные (в частности, горизонтальные) асимптоты - смотри приложение.
10. Дополнительные точки, позволяющие более точно построить график - даны в приложении.
11. Построение графика функции по проведенному исследованию дан в приложении.
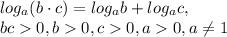
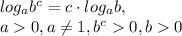
(x^2+(3b+2)X+2b^2 +3b+1) / (x^2 - 5x +4)=0
(x²+(3b+2)x+2b² +3b+1) / (x² - 5x +4)=0 ;
ОДЗ: x² - 5x +4≠0 ⇒ [ x ≠ 1 ; x ≠ 4.
---
x²+(3b+2)x+2b² +3b+1=0 ;
D=(3b+2)² - 4(2b² +3b+1)= b² ≥ 0 всегда имеет решения :
x₁ = (-3 b- 2 - b)/2 = -1 - 2b , если -1 - 2b ≠ 1 и -1 - 2b ≠ 4 ,
т.е. если b ≠ -1 и b ≠ -2,5.
x₂ = (- 3b - 2 +b)/2 = -1 - b , опять если -1 - b ≠ 1 b и -1 - b ≠ 4 , .
т.е. если b ≠ -2 и b ≠ - 5.
* * * * P.S.
Можно было в самом начале для уравнения x²+(3b+2)x+2b² +3b+1=0 исключить x =1 и x = 4 в качестве корней;
1) 1²+(3b+2)1+2b² +3b+1=0 ⇔2b² +6b+4 =0⇔
b² +3b+2 =0 ⇒[ b = -2 ; b = -1 .
2) 4²+(3b+2)4+2b² +3b+1=0⇔2b² +15b+25 =0⇔ [ b = -5 ; b = - 2,5 .
b ≠ -5 ; -2,5 ; -2 ; - 1.