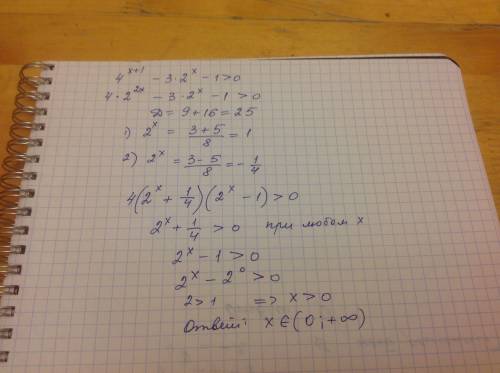
Пусть х - цифра десятков;
у - цифра единиц .
По условию цифра десятков, увеличенная на 2, в 2 раза больше цифры единиц.
Исходя из этого, получаем первое уравнение:
х +2 = 2у
Ещё в условии сказано, что если цифры десятков и единиц поменять местами, то полученное число будет меньше первоначального на 27, т.е.
(10х+у) > (10у+х) на 27
Получаем второе уравнение:
(10х+у ) - (10у+х) = 27
Упростим это уравнение:
9х - 9у = 27
х - у = 3
Решаем систему:
{x + 2 = 2y
{x - y = 3
Из второго уравнения выразим х:
х = у + 3
Подставим в первое:
у + 3 + 2 = 2у
у = 5 - цифра единиц
х = 5 + 3
х = 8 - цифра десятков;
ответ: 85
Решение
1) < 1 = 110° ; < 1 = < 3 = 110° , как вертикальные углы
<1 + <2 = 180° , как смежные, < 2 = 180° – 110° = 70°
<2 = <4 = 70° , как вертикальные углы
<4 = < 6 = 70° как внутренние накрест лежажие углы при параллельных прямых a и b и секущей с
<3 = <5 = 110° как внутренние накрест лежажие углы при параллельных прямых a и b и секущей с
<5 = <8 = 110° , как вертикальные углы
<6 = <7 = 700 , как вертикальные углы.
2) Пусть <2 = x , тогда <1 = x + 40.
По свойству смежных углов получаем уравнение
x + x + 40 = 180
2x = 140
x = 70
< 2 = 70°
< 1 = 70° + 40° = 110°
3) Сумма внутренних односторонних углов равна 1800.
<3 + <6 = = 180°
<3 - <6 = 70°
2*(<3) = 180° + 70°
2*(<3) = 250°
<3 = 125°
<6 = 180° – 125° = 55°
<1 = < 3 = 125° , как вертикальные углы
<1 + <2 = 180° , как смежные,
< 2 = 180° – 125° = 55°
<2 = <4 = 55° , как вертикальные углы
<4 = < 6 = 55° как внутренние накрест лежажие углы при параллельных прямых a и b и секущей с
<3 = <5 = 125° как внутренние накрест лежажие углы при параллельных прямых a и b и секущей с
<5 = <8 = 125° , как вертикальные углы
<6 = <7 = 55° , как вертикальные углы.
2^x=a
4a²-3a-1>0
D=9+16=25
a1=(3-5)/8=-1/4 U a2=(3+5)/8=1
a<-1/4 U a>1
2^x<-1/4 нет решения 2^x>1
x>0
x∈(0;∞)