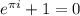
Это тождество Эйлера, являющееся частным случаем формулы Эйлера 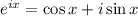 при
при  .
.
Тождество объединяет между собой пять фундаментальных чисел из разных областей математики, связь между которыми на первый взгляд неочевидна:
1) основание натурального логарифма  (алгебра);
(алгебра);
2) отношение длины окружности к ее диаметру 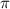 (геометрия);
(геометрия);
3) мнимую единицу  (комплексные числа);
(комплексные числа);
4) нейтральный элемент относительно умножения 1 (арифметика);
5) нейтральный элемент относительно сложения 0 (арифметика).
Тождество примечательно в первую очередь своей простотой и элегантностью. Так, Ричард Фейнманн называл его "самой замечательной формулой в математике".
Примечательна фраза профессора Гарвардского университета Бенджамин Пирса, произнесенная после доказательства тождества Эйлера: "мы не можем понять её [формулу], и мы не знаем, что она значит, но мы доказали её, и поэтому мы знаем, что она должна быть достоверной".
12p^4 - 11p^3 + 54p^2 + 10p - 25.
Объяснение:
1. Выполним умножение: каждое слагаемое первого трехчлена поочередно умножим на каждое слагаемое второго трехчлена, результаты сложим, учитывая знаки.
(p^2 − p + 5)(12p^2 + p − 5) = p^2 × 12p^2 + p^2 × p - p^2 × 5 - p × 12p^2 - p × p + p × 5 + 5 × 12p^2 + 5 × p - 5 × 5 = 12p^4 + p^3 - 5p^2 - 12p^3 - p^2 +5p + 60p^2 + 5p - 25 = 12p^4 - 11p^3 + 54p^2 + 10p - 25.
2. Приведем подобные слагаемые, поочередно сложив коэффициенты переменных одной степени.
12p^4 - 11p^3 + 54p^2 + 10p-25