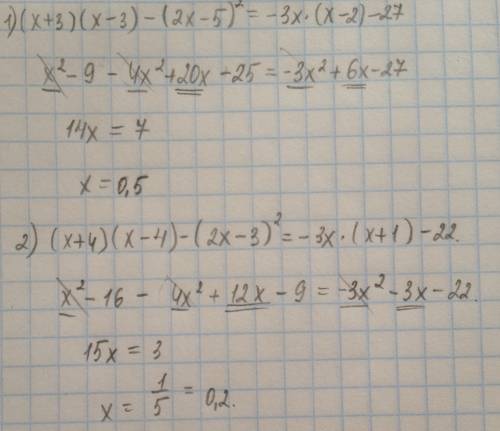
Пусть х км/ч - скорость второго велосипедиста, тогда (х+1) км/ч - скорость первого велосипедиста, 240/x (ч) - время второго велосипедиста, 240/(х+1) (ч) - время первого велосипедиста. Зная, что первый велосипедист прибыл к финишу на 1 час раньше второго, составим и решим уравнение:
240/х-240/(х+1)=1
приведем к общему знаменателю: (240х+240-240х-х(х+1))/х(х+1)=0
(240-x^2-x)/x(x+1)=0
Найдем ОДЗ и избавимся от знаменателя: х не равно 0 и х не равно -1
-х^2-x+240=0 умножим на -1: x^2+x-240=0
D=1-4*1*(-240)=1+ 960=961
x1=(-1-31)/2=-32/2=-16 - не удовлетворяет условию задачи
x2=(-1+31)/2=30/2=15
т.е. 15 км/ч - скорость второго велосипедиста, тогда скорость первого: 15+1=16(км/ч)
ответ: 16 км/ч
Отсюда имеем

Это решение исходной системы.
Вернемся к уравнению
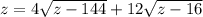
Для того, чтобы была хоть какая-то польза, представим его в виде
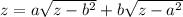
Решение
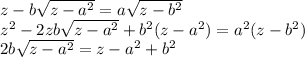
Вот оно, то самое место, где минус в первоначальном уравнении для z приводит к нерешаемому уравнению (в действительных числах). В случае минуса правая часть будет с другим знаком, и мы получаем равенство отрицательной и положительной величин. Однако в случае плюса ничего такого нет, и мы смело возводим обе ЗАВЕДОМО положительные величины в квадрат. Получаем.
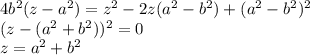
Подставляем а = 4 и b = 12, получаем решение.