sin20+sin40-cos10=0
Сложим синусы по формулам суммы:
2sin30*cos10-cos10=0
Вынесем общий множитель:
cos10(2sin30-1)=0
Произведение равно 0, когда хотя бы один из множителей равен 0, в данном случае
(2sin30-1)=(2*1/2-1)=0
2.sin3a-sina*cos2a
По формулам произведения умножим синус на косинус:
sin3a-1/2 (sin(-a)+sin3a)=sin3a+1/2 sina - 1/2 sin3a=1/2(sin3a+sina)
По формулам суммы сложим синусы:
1/2(sin3a+sina)=1/2*2sin2a*cosa=sin2a*cosa=2sina*cosa*cosa=2sina*cos^2 a
3.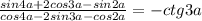
Т.к. в правой части ничего изменить нельзя, то будем работать только с левой части уравнения, пытаюсь представить ее в виде -ctg3a.
В числители вычтем синусы, в знаменателе - косинусы.
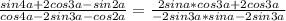
Вынесем в числителе и знаменателе общий множитель:
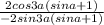
Сокращаем и получаем -cos3a/sin3a=-ctg3a