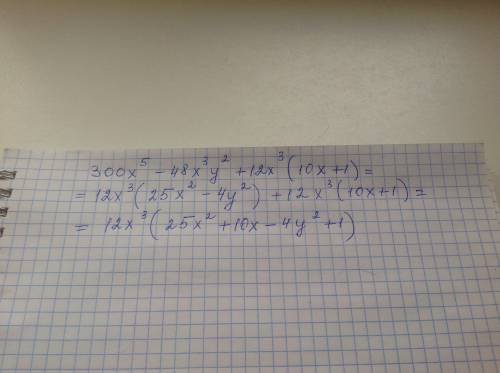
Чтобы изобразить график линейной функции вида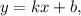 
где 
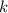и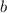 
— коэффициенты, достаточно на координатной плоскости отметить две точки и провести через них прямую.
Для этого строят таблицу для двух точек: первая строка — абсцисса (иксы), вторая строка — ордината (игреки). Вы — хозяин своей таблицы. Подбирайте любое значение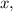 
подставляйте его в функцию и находите 
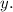(Подбирайте числа в пределах разумного.)
Пример. Изобразить график линейной функции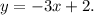 
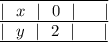
Строим таблицу для двух точек:
Пусть 
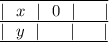
Тогда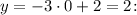 
Пусть 
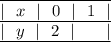
Тогда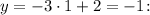 
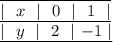
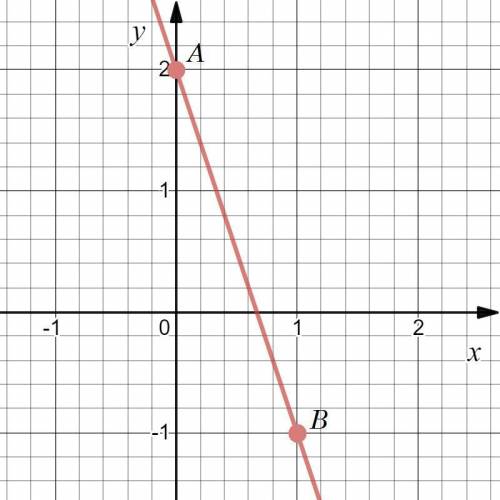
Имеем заполненную таблицу для двух точек. Изобразим координатную плоскость, отметим две точк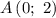и: 
и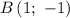 
— и проведем через них прямую (см. вложение). График линейной функции 
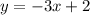построен.
пусть первое число равно х, а второе у. Тогда 2х+у=11, а x^2+y^2=25.
Получаем систему уравнений:
2х+у=11;
x^2+y^2=25.
Выразим из первого уравнения у:
у=11-2х
и подставим полученное значение во втрое:
x^2+(11-2x)^2=25
x^2+121-44x+4x^2=25
5x^2-44x+121-25=0
5x^2-44x+96=0
Найдем дискриминант квадратного уравнения
D=b^2-4ac=1936-4*5*96=16
Так как дискриминант больше нуля то, квадратное уравнение имеет два корня:
x1=(-b+√D)/(2a)=(44+√16)/(2*5)=4.8
x2=(-b-√D)/2a=(44-√16)/(2*5)=4
В условии задачи сказано, что взяты натуральные числа, значит, нам подходит только х=4
Найдем у:
у=11-2х
у=11-2*4
у=3
ответ: взяты числа 4 и 3
