1) f '(x) = 2sinx·cosx - cosx = sin2x -sin (π/2 -x)
f '(x) = 0 ⇔ sin2x = sin (π/2 -x) ⇔ 2x = π/2 -x + 2πn , n∈Z или
2x = π - π/2 +x + 2πk , k ∈Z ⇔
x = π/6 + 2πn/3 , n∈Z или x = π/2 + 2πk, k ∈Z
2) f '(x ) = 4cosx - 3sinx - 5 = 0 ⇔ 4cosx - 3sinx = 5 ⇔
cosx ·4/5 - sinx·3/5 = 1 ;
Пусть соsα = 4/5 ; sinα = 3/5 ; α ∈ ( 0 ; π/2) ;
cosx·cosα - sinx·sinα = 1 или :
cos(x + α ) = 1 ⇔ x +α = 2πn ; n ∈Z ⇔ x = - arccos 4/5 + 2πn ; n ∈ Z
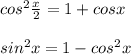
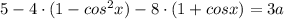
Получаем квадратное уравнение относительно
cosx=t
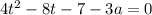
Это уравнение имеет хотя бы один корень, если D ≥0
D=64+16(7+3a)=16(11+3a)
D≥0⇒ 11+3a≥0⇒ a≥ -11/3
t₁=1- (√(11+3а))/2 или t₂=1+ (√(11+3а))/2
Обратная замена приводит к уравнениям вида cos=t₁ или cosx=t₂
Чтобы эти уравнения имели хотя бы один корень, необходимо, что бы
-1 ≤ t₁ ≤1 или -1 ≤ t₂ ≤1
Решаем неравенства:
-1 ≤1+ (√(11+3а))/2 ≤1
-2≤√(11+3а))/2≤0
-4≤√(11+3а)≤0
Решением неравенства является
11+3a=0
a=-11/3
t₁=t₂=1/2
cosx=1/2
x=±(π/3)+2πn, n∈Z
Неравенство
-1 ≤1- (√(11+3а))/2 ≤1
также приводит к ответу a=-11/3
О т в е т. При а=-11/3
x=±(π/3)+2πn, n∈Z
Во втором примере у Вас опечатка (5z), поэтому рассматриваю 2 случая (под буквами a и b). При этом первый решаю с метода универсальной тригонометрической подстановки, где :
: