Объяснение: Щоб знайти найбільше і найменше значення функції на відрізку, треба
а) знайти максимуми і мінімуми функції на цьому відрізку. Для цього беруть похідну і прирівнюють її до 0. Рішення і є критичними точками.
б) знайти значення функції на кінцях відрізку.
в) вибрати найбільше і найменше значення функції.
3. а) g'(x)=(-x²+6x-1)'= -2x+6
g'(x)=0, -2x+6=0, -2x=-6, x=3
g(3)= -3²+6·3-1=-9+18-1=8, g(3)=8
б) [2;4]
g(2)=-2²+6·2-1=-4+12-1=7, g(2)=7
g(4)=-4²+6·4-1=-16+24-1=7, g(4)=7
в) Найбільше значення функції g(3)=8
Найменше значення функції g(2)=7 і g(4Объяснение: Щоб знайти найбільше і найменше значення функції на відрізку, треба
а) знайти максимуми і мінімуми функції на цьому відрізку. Для цього беруть похідну і прирівнюють її до 0. Рішення і є критичними точками.
б) знайти значення функції на кінцях відрізку.
в) вибрати найбільше і найменше значення функції.
3. а) g'(x)=(-x²+6x-1)'= -2x+6
g'(x)=0, -2x+6=0, -2x=-6, x=3
g(3)= -3²+6·3-1=-9+18-1=8, g(3)=8
б) [2;4]
g(2)=-2²+6·2-1=-4+12-1=7, g(2)=7
g(4)=-4²+6·4-1=-16+24-1=7, g(4)=7
в) Найбільше значення функції g(3)=8
Найменше значення функції g(2)=7 і g(4)=7
1) x∈(1;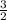 
)
2) x∈(-∞; -3)∪(1; +∞)
Объяснение первого неравенства:
Чтобы произведение было меньше нуля, множители должны иметь разные знаки. Тогда получаем две системы (знака системы сайт не имеет, строчки должны быть объединены фигурной скобкой).
Первая:
x-1<0
2x-3>0
Вторая:
x-1>0
2x-3<0
Решение первой:
x-1<0
x<1;
2x-3>0
2x>3
x>;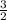
Поскольку мы решали систему, нужно найти пересечение решений. Здесь пересечение - пустое множество, потому что 3/2 больше 1.
Решение второй:
x-1>0
x>1;
2x-3<0
2x<3
x<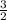
Пересечение решений - x∈(1; 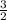) (скобки ставим круглые, потому что знак неравенства строгий)
Объяснение второго неравенства:
Чтобы произведение было больше нуля, множители должны иметь один знак. Тогда получаем две системы:
Первая:
x+3>0
x-1>0
Вторая:
x+3<0
x-1<0
Решение первой:
x+3>0
x>-3;
x-1>0
x>1;
Пересечение: x∈(1; +∞)
Решение второй:
x+3<0
x<-3;
x-1<0
x<1;
Пересечение: x∈(-∞; -3)
Пересекаем решения первой и второй систем и получаем: x∈(-∞; -3)∪(1; +∞)
б) (2а + 0,5)² =4а²+2а+0,25
в) (-3а + 2в)² =9а²-12ав+4в²
г) (х² - у²)²=х∧4-2х²у²+у∧4
д) (у + 15)² =у²+30у+225
е) (5х - 0,2)² =25х²-2х+0,04
ж) (-2а + 7в)² =4а²-28ав+49в²
з) (а³ + в³)