Построить график функции f(x)=log3(x)+3. определить область определения d(f) и область значения e(f).

👇

Ответ:

dasha29saranina1234

28.11.2021

F=log3 (x)+3 x>0 -∞ < f<∞

Построить график функции f(x)=log3(x)+3. определить область определения d(f) и область значения e(f)

4,4(65 оценок)

Открыть все ответы

Ответ:

Zikeev2007

28.11.2021

$\sqrt[5]{32a^7} \cdot \sqrt[5]{a^3} = 2\sqrt[5]{a^7} \cdot a^{\frac{3}{5}} = 2a^{\frac{7}{5}} \cdot a^{\frac{3}{5}} = 2a^{\frac{7}{5} + \frac{3}{5}} = 2a^{\frac{10}{5}} = \boxed{2a^2}$ .

ответ: В.

$\dfrac{1}{3}\sqrt[3]{-147} \cdot \sqrt[3]{-63} = \dfrac{1}{3}\cdot (-\sqrt[3]{147})\cdot (-\sqrt[3]{63}) = \dfrac{1}{3}\sqrt[3]{147\cdot 63} = \dfrac{\sqrt[3]{9261}}{3} = \dfrac{21}{3} =\\\\\\= \boxed{\textbf{7}}$

ответ: А.

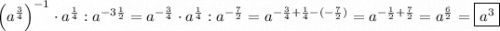
$\left (a^{\frac{3}{4}}\right )^{-1} \cdot a^{\frac{1}{4}} : a^{-3\frac{1}{2}} = a^{-\frac{3}{4}} \cdot a^{\frac{1}{4}} : a^{-\frac{7}{2}} = a^{-\frac{3}{4} + \frac{1}{4} - (-\frac{7}{2})} = a^{-\frac{1}{2} + \frac{7}{2}} = a^{\frac{6}{2}} = \boxed{a^3}$

ответ: Г.

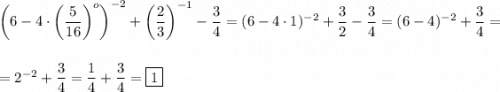
$\left (6 - 4\cdot \left(\dfrac{5}{16}\right )^o\right )^{-2} + \left (\dfrac{2}{3}\right )^{-1} - \dfrac{3}{4} = (6-4\cdot 1)^{-2} + \dfrac{3}{2} - \dfrac{3}{4} = (6-4)^{-2} + \dfrac{3}{4} =\\\\\\= 2^{-2} + \dfrac{3}{4} = \dfrac{1}{4} + \dfrac{3}{4} = \boxed{1}$

ответ: А.

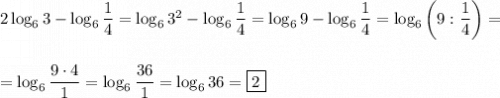
$2\log_{6}3 - \log_{6}\dfrac{1}{4} = \log_{6}3^2 - \log_{6}\dfrac{1}{4} = \log_{6}9 - \log_{6}\dfrac{1}{4} = \log_{6}\left (9 : \dfrac{1}{4}\right ) =\\\\\\= \log_{6}\dfrac{9\cdot 4}{1} = \log_{6}\dfrac{36}{1} = \log_{6}36 = \boxed{2}$

ответ: А.

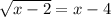
$\sqrt{x-2} = x-4$

Для начала решим систему неравенств, определяющую область допустимых значений :

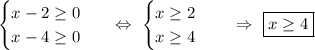
$\begin{equation*}\begin{cases}x - 2\geq 0\\x - 4\geq 0\end{cases}\end{equation*}\ \ \ \Leftrightarrow\ \begin{equation*}\begin{cases}x \geq 2\\x \geq 4\end{cases}\end{equation*}\ \ \ \ \Rightarrow\ \boxed{x\geq 4}$

Возводим обе части уравнения в квадрат.

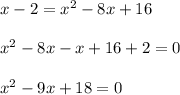
$x - 2 = x^2 - 8x + 16\\\\x^2 - 8x - x + 16 + 2 = 0\\\\x^2 - 9x + 18 = 0$

По теореме Виета:

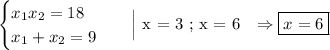
$\begin{equation*}\begin{cases}x_{1}x_{2} = 18\\x_{1}+x_{2} = 9\end{cases}\end{equation*}\ \ \ \Big| x = 3 ; x = 6\ \ \ \Rightarrow \boxed{x=6}$

3 не подходит под область допустимых значений.

ответ: корень только один, и он положительный.

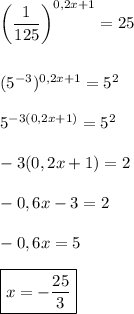
$\left (\dfrac{1}{125}\right )^{0,2x+1} = 25\\\\\\(5^{-3})^{0,2x+1} = 5^2\\\\5^{-3(0,2x+1)} = 5^2\\\\-3(0,2x+1) = 2\\\\-0,6x - 3 = 2\\\\-0,6x = 5\\\\\boxed{x = -\dfrac{25}{3}}$

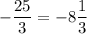$-\dfrac{25}{3} = -8\dfrac{1}{3}$ , тогда корень принадлежит промежутку (-9; -7] .

ответ: (-9; -7] .

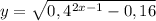
$y = \sqrt{0,4^{2x-1} - 0,16}$

Областью определения функции является решение следующего неравенства:

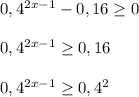
$0,4^{2x-1} - 0,16 \geq 0\\\\0,4^{2x-1} \geq 0,16\\\\0,4^{2x-1} \geq 0,4^2$

Так как основание меньше единицы, то:

$2x - 1\leq 2\\\\2x \leq 3\\\\x \leq 1,5\ \ \ \ \Rightarrow \boxed{x\in(-\infty; 1,5]}$

ответ: $(-\infty; 1,5]$ .

Найдём область значения функции. 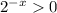$2^{-x} 0$ , тогда 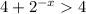$4+2^{-x} 4$ . Значит, 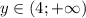$y \in (4; +\infty)$ . Следовательно, из перечисленных чисел в множество значений входит только 5 (4 не входит, так как концы не включаем).

ответ: 5.

10)

Условие чётности функции: 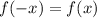f(-x) = f(x) . Проверяем для каждой.

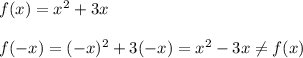$f(x) = x^2 + 3x\\\\f(-x) = (-x)^2 + 3(-x) = x^2 - 3x \neq f(x)$ - не подходит.

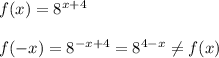$f(x) = 8^{x+4}\\\\f(-x) = 8^{-x+4} = 8^{4-x} \neq f(x)$ - не подходит.

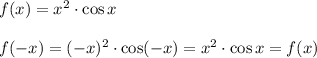$f(x) = x^2\cdot \cos x\\\\f(-x) = (-x)^2 \cdot \cos(-x) = x^2 \cdot \cos x = f(x)$ - подходит.

ответ: 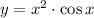$y = x^2\cdot \cos x$ .

4,5(49 оценок)

Ответ:

кар91

28.11.2021

1.а)x^2-12*x+36
б)y^2+8*y+16
в)a^2-64
г)9*x^4-54*x^2+81
д)(256*y^2+32*y+1)/4
е)(-0.04*(16*x^2-225*a^10)
ё)8*y^3+12*y^2+6*y+1
ж)d^2+6*c*d+9*c^2
з)81*h^2-90*h+25
и)-16*q^4-4*q^3+4*q+1

2.а)(у-5)(у+5)+25=y^2-25+25=y^2
б)(5х-6)в квадрате - 25 х в квадрате =25x^2-60x+36-25x^2=36-60x
в)(5а-7)в квадрате - (3а-2)(3а+2)=25a^2-70a+49-9a^2+4=16a^2-70a+51
г) (1/7м + 14н)в квадрате - (3н+1/7м)в квадрате=(m^2+196*h*m+9604*h^2)/49-(m^2+42*h*m+441*h^2)/49=(22*h*m+1309*h^2)/7

3 (3х-2)(3х+2)-5х=(9х+7)(х-1)
9X^2-4-5x=9x^2-2x-7
-3x=-3
x=1
проверка: 1*5-5=16*0
0=0

4 (n+5)^2-n^2=n^2+10n+25-n^2=5(2n+5) , 5 делится на 5, 2н - это честное число при любых н, любое четное чилос делится на 5 , значит и все это выражение делится на 5 при любых н

4,5(71 оценок)

Это интересно:

Семейная-жизнь

11.01.2022

Как рассказать парню о беременности после случайного секса?...

Здоровье

12.08.2021

Избавление от боли в зубе мудрости: легкий и безболезненный способ...

Компьютеры-и-электроника

14.06.2022

Как отключить голосовое управление iPhone: простые шаги для пользователей...

Здоровье