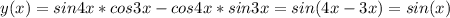
 есть
есть 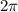
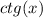 равен
равен 
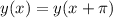
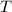 - искомый период, тогда
- искомый период, тогда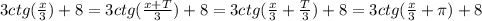
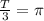

 относительно оси OX на 8 единиц вверх, также не влияя на период
относительно оси OX на 8 единиц вверх, также не влияя на период

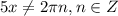
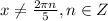
 - это симметричное относительно начала координат множество точек,
- это симметричное относительно начала координат множество точек, также симметрична относительно начала координат. Это означает, что есть смысл проверять функцию на парность, дальше.
также симметрична относительно начала координат. Это означает, что есть смысл проверять функцию на парность, дальше.
на второй х-2