Тест 1 (на оценку “3”) 1. Раскрыть скобки: (х – у)2 а) х2 – 2хy + у2 б) х2 – ху + у2 в) х2 – у2 г) х2 – 2хy – у2 2. Упростить выражение: (а + 3в)(3в – а) а) 9в2 + а2 б) 9в2 – а2 в) а2 – 9в2 г) а2 – 6ав + 9в2 3. Разложить на множители: 4х2 – 64у2 а) (4х – 64у)(4х + 64у) б) (8у – 2х)(8у + 2х) в) (2х – 8у)(2х + 8у) г) разложить нельзя Тест 2 (на оценку “4”) 1. Упростить выражение: 6а + (4а – 3)2 а) 16а2 + 30а + 9 б) 16а2 – 18а + 9 в) 16а2 – 30а + 9 г) 16а2 + 18а + 9 2. Упростить выражение: (а + 0,3в)(0,3в – а) а) 0,9в2 – а2 б) 0,09в2 – а2 в) 0,09в2 + а2 г) а2 – 0,09в2 3. Упростить выражение: (а – 0,3)(а2 + 0,3а + 0,09) а) а3 – 0,27 б) а3 – 0,027 в) а3 + 0,27 г) а3 + 0,027 Тест 3 (на оценку “5”) 1. Упростить выражение: (а – 5)(а2 + 5а + 25) а) а3 – а2 + 25 б) а3 – 125 в) а3 + 125 г) а3 + а2 + 25 2. Упростить выражение: (3х – 2)(3х + 2) – (1 + х)(х – 1) а) 8х2 – 3 б) 8х2 + 3 в) 9х2 – 3 г) 8х2 – 5 Проводит рефлексию. — Понравился ли вам урок? — Что было трудным для вас? — Что вам больше понравилось? Ученики показывают свои знания. Оценивают работу своих одноклассников. На стикерах записывают свое мнение по поводу урока. Ромашка Блума
Источник: https://uroky.kz/algebra-10-klass-kratkosrochnyj-plany-ksp/
Объяснение:
По определению, 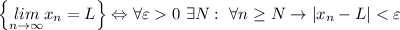
Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение 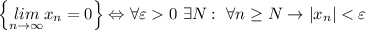
2) 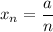
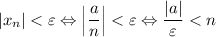
А значит, если взять ![N=\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/0d89e.png) (*),
(*),  . И правда:
. И правда: 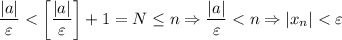
(*) Очевидно, что для любого допустимого значения  выражение
выражение ![\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/ae843.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
А это и означает, что предел данной последовательности равен 0
4) 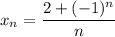

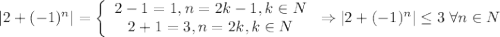
А значит, если взять ![N=\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/a4ca4.png) (**),
(**),  . И правда:
. И правда: ![\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|](/tpl/images/3820/0626/49458.png)
(**) Очевидно, что для любого допустимого значения  выражение
выражение ![\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/698f8.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
А это и означает, что предел данной последовательности равен 0
___________________________
2) a=1. Тогда 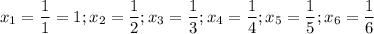
4)

___________________________
Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x. 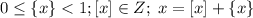

а)
После того, как шар был вынут и возвращен на место шансы вынуть шар распределены по цветам так же, как были распределены до этого.
Данная вероятность будет равна 1-(вероятность того, что все три шара имеют одинаковый цвет).
Если N-16>2 и 36-N>2, то эта вероятность равна:
Если N-16<3 то эта вероятность равна:
Если 36-N<3 то эта вероятность равна:
б)
После того, как шар был вынут, число шаров уменьшится, как и число шаров того же цвета, что и предыдущий, поэтому формула слегка поменяется:
Если N-16>2 и 36-N>2, то эта вероятность равна:
Если N-16<3 то эта вероятность равна:
Если 36-N<3 то эта вероятность равна: