Повар Миша может выполнить заказ на 136 минут быстрее, чем повар Коля.
Совместно они выполняют заказ за 51 минуту.
Пусть x минут - выполняет заказ повар Коля, тогда
x + 136 - выполняет заказ повар Миша
За 1 минуту совместной работы они выполнят 1/x + 1/(x+136) заказа.
Составим уравнение:
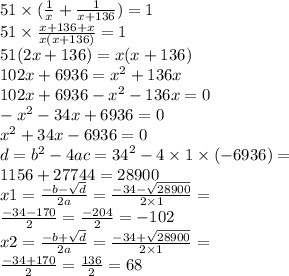
Решив данное уравнение ,получим x= - 102 и x= 68. По условию задачи x – величина положительная. Следовательно, повар Коля сможет выполнить работу за 68 минут, а повар Миша (68 + 136 = 204) за 204 минуты.
ответ: Коля выполнит заказ за 68 минут, Миша выполнит заказ за 204 минуты
Введем подстановку t = cos (3x), где |t| меньше или равен 1, т.к. функция cosx является ограниченной снизу -1, сверху +1.
Тогда исходное уравнение перепишется следующим образом:
2t^2 - 5t - 3 = 0.
Сейчас перед нами обыкновенное квадратное уравнение. Находим дискриминант и корни, если они будут.
D = b^2 - 4ac,
D = 25 + 24 = 49,
D>0 и значит уравнение имеет два корня.
t1 = (-b - корень из D) / (2a),
t1 = (5 - 7) / 4 = -1/2;
t2 = (-b + корень из D) / (2a),
t1 = (5 + 7) / 4 = 3;
Вернемся к подстановке t = cos (3x):
1) cos (3x) = -1/2,
3x = ± (2pi) / 3 + 2pi*k, где k - целое число;
x = ± (2pi)/9 + (2pi*k) / 3, где k - целое число.
2) cos (3x) ≠ 3, т.к. |t| ≤ 1.
ответ: x = ± (2pi)/9 + (2pi*k) / 3, где k - целое число.
(2a)³-1³ =( 2* (-1/3))³ -1=-8/27 -1= -1. 8/27