Question

Даны точки а (4; 8), в (2; -2), 1)найдите координаты середины отрезка ав 2) найдите длину отрезка ав 3) определите какая из данных точек принадлежит прямой х-у+4=0

Answer 1

Координаты отрезка AB: AB = {2-4; -2-8} = {-2; -10}.

1) Координаты середины отрезка АВ ищем по следующим формулам:

$\sf x=\dfrac{x_A+x_B}{2};~~~~~~~~ y=\dfrac{y_A+y_B}{2}$

Обозначим точку М - середину отрезка АВ.

$\sf x_M=\dfrac{2+4}{2}=3;~~~~~~~~~y_M=\dfrac{8-2}{2}=3$

M(3;3).

2) Длина отрезка АВ: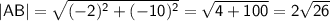 $\sf |AB|=\sqrt{(-2)^2+(-10)^2}=\sqrt{4+100}=2\sqrt{26}$

3) Подставим координаты точек A(4;8) и B(2;-2) в уравнение прямой, имеем:

x=4; y=8;  ⇒  4-8+4=0    ⇔   0 = 0  ⇒  точка А принадлежит прямой

x=2; y=-2;  ⇒  2+2+4=0    ⇔   8 ≠ 0  ⇒  точка B не принадлежит прямой