Алгебра: нужно к завтрашнему , ! буду вам -

1) Возьмём числитель первой дроби за X. Тогда знаменатель будет равен X+3. Первая дробь будет равна Если увеличить числитель первой дроби на два и знаменатель на четыре, то вторая дробь будет равна В условии задания сказано, что вторая дробь больше первой на , значит разность второй и первой дроби будет равна одной восьмой. Составим уравнение. - = Чтобы избавиться от дробей умножаем каждое число на (x+7)·(x+3)·8(x+2)·(x+3)·8 - x·(x+7)·8=(x+7)·(x+3)(x²+3x+2x+6)·8 - (x²+7x)·8=(x+7)·(x+3)8x²+24x+16x+48-8x²-56x=x²+3x+7x+21...

нужно к завтрашнему , ! буду вам -

👇

Увидеть ответ

Ответ:

Tanya6164

25.07.2021

0,5y-1,5-6+4,5y-7,5=0
5y-15=0
y=3

4,7(29 оценок)

Ответ:

daniilsemkin05

25.07.2021

Умножаем и составляем уравнение:
0,5*(у-3)=3*(2-1,5у)+7,5
0,5у-1,5=6-4,5у+7,5
переводим числа с "у" в одну сторону числа в другую...
0,5у+4,5у=6+7,5+1,5
5у=15
у=15:5
у=3
ответ: 3

4,6(78 оценок)

Открыть все ответы

Ответ:

рогозина

25.07.2021

Выражение: 51*cos(4)/sin(86)+8

ответ: 51*cos(4)/sin(86)+8

По шагам:
1. 51*0.997564050259824/sin(86)+8
1.1. cos(4)=0.997564050259824
2. 50.875766563251/sin(86)+8
2.1. 51*0.997564050259824~~50.875766563251
X0.997564050259824
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _5_1_ _
0997564050259824
4_9_8_7_8_2_0_2_5_1_2_9_9_1_2_0_ _ _
50.875766563251024
3. 50.875766563251/0.997564050259824+8
3.1. sin(86)=0.997564050259824
4. 51+8
4.1. 50.875766563251/0.997564050259824~~51
50.875766563251000|0_._9_9_7_5_6_4_0_5_0_2_5_9_8_2_4_ _
4_9_8_7_8_2_0_2_5_1_2_9_9_1_2_0_ |50.9
9975640502598000
8_9_7_8_0_7_6_4_5_2_3_3_8_4_1_6_
997564050259584
5. 59
5.1. 51+8=59

4,7(44 оценок)

Ответ:

artemkafire2005

25.07.2021

1) Возьмём числитель первой дроби за X. Тогда знаменатель будет равен X+3. Первая дробь будет равна 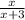$\frac{x}{x+3}$ Если увеличить числитель первой дроби на два и знаменатель на четыре, то вторая дробь будет равна 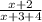$\frac{x+2}{x+3+4}$ В условии задания сказано, что вторая дробь больше первой на 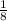$\frac{1}{8}$ , значит разность второй и первой дроби будет равна одной восьмой. Составим уравнение.

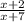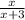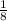$\frac{x+2}{x+7}$ - $\frac{x}{x+3}$ = $\frac{1}{8}$ Чтобы избавиться от дробей умножаем каждое число на (x+7)·(x+3)·8

(x+2)·(x+3)·8 - x·(x+7)·8=(x+7)·(x+3)

(x²+3x+2x+6)·8 - (x²+7x)·8=(x+7)·(x+3)

8x²+24x+16x+48-8x²-56x=x²+3x+7x+21 Переносим всё в левую сторону и приравниваем выражение к нулю. Упростив, получим:

-x²-26+27=0

D=676+108=784;28²

D>0

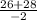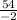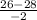x1= $\frac{26+28}{-2}$ = $\frac{54}{-2}$ = -27

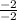x2= $\frac{26-28}{-2}$ = $\frac{-2}{-2}$ =1

Так как у нас получилось два корня, нужно подставить получившиеся значение в исходное выражение и найти верный ответ.

а) Возьмём первый корень, равный -27 и подставим в изначальное выражение.

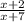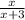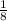
$\frac{x+2}{x+7}$ - $\frac{x}{x+3}$ = $\frac{1}{8}$

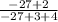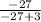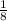
$\frac{-27+2}{-27+3+4}$ - $\frac{-27}{-27+3}$ = $\frac{1}{8}$

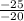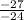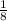
$\frac{-25}{-20}$ - $\frac{-27}{-24}$ = $\frac{1}{8}$

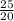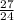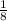
$\frac{25}{20}$ - $\frac{27}{24}$ = $\frac{1}{8}$

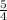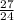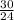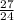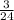
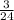$\frac{5}{4}$ - $\frac{27}{24}$ = $\frac{30}{24}$ - $\frac{27}{24}$ = $\frac{3}{24}$

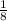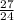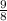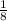
$\frac{3}{24}$ = $\frac{1}{8}$ ⇒ Корень -27 подходит. Значит изначальная дробь равна $\frac{27}{24}$ = $\frac{9}{8}$ =1 $\frac{1}{8}$

б) Возьмём второй корень, равный 1 и подставим в изначальное уравнение

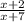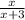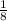
$\frac{x+2}{x+7}$ - $\frac{x}{x+3}$ = $\frac{1}{8}$

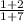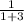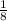
$\frac{1+2}{1+7}$ - $\frac{1}{1+3}$ = $\frac{1}{8}$

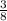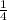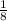
$\frac{3}{8}$ - $\frac{1}{4}$ = $\frac{1}{8}$

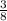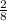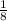$\frac{3}{8}$ - $\frac{2}{8}$ = $\frac{1}{8}$ ⇒ Корень 1 также подходит. Значит исходное уравнение равно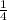 $\frac{1}{4}$

Так как при проверке оба корня оказались верны, то в ответе будет две дроби.

2) $\left[\begin{array}{ccc}S&U&t\\200&x&\\200&x+10&\end{array}\right]$

Рассмотрим движение машины в двух случаях: Как она должна была двигаться изначально и как она двигалась в итоге. Путь, пройденный автомобилем, не изменился. Скорость увеличилась на 10 км/ч. Так как автомобиль прибыл быстрее запланированного, то разница между временем, затраченным в первом случае, и временем, затраченным во втором случае, будет равна 1 часу. Составим уравнение.

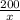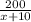$\frac{200}{x}$ - $\frac{200}{x+10}$ =1 Избавимся от дробей, умножив каждое число на x·(x+10)