Наверное за это и не зачли правильный ответ .
В 3 пункте вы спутали с решением неполного квадратного уравнения.
Например, при решении уравнения х²=225 , обычно пишут х=+/- 15 . И это верно. Просто упускают запись: √х²=√225 ⇒ |x|=15 , пользуясь правилом, что √х²=|x| .
А из |x|=15 следует, что "х" может равняться либо 15, либо (-15) , то есть х=+/-15 , так как модуль положительного числа равен самому числу: |15|=15 , а модуль отрицательного числа равен числу, ему противоположному: |-15|=15 .
Фактически после записи х²=225 надо писать +/- х=15 , так как √225=15, а потом уже х=+/-15 .
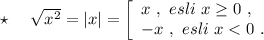
Объяснение:
=> , 
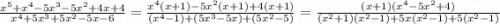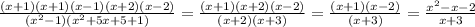, пояснение 1) 
; 
=> 
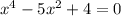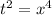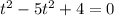
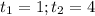
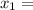±1 ; 
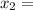±2 тогда уравнение 
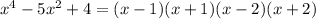2) 
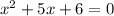x1=-3 ; x2=-2 =>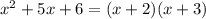 
3ˣ+3*3ˣ=4
4*3ˣ=4
3ˣ=1
х=0
√(3х+1)=х-3 ОДЗ 3х+1>0 x>-1/3
возведем обе части в квадрат
3х+1=(х-3)²
3х+1=х²-6х+9
х²-9х+8=0
D=81-32=49 √D=7
х₁=(9+7)/2=8
х₂=(9-7)/2=1