Question

Найдите целые корни многочлена и разложите его на множители x^3+3x-234

Answer 1

Можно разложить на множители  по методу Горнера 
х³+3х-234 поделим уголком на х-6
тогда получится х²+6х+39
запишем   х³+3х-234=(х-6)(х²+6х+39)
(х-6)(х²+6х+39)=0
мы знаем ,что если хотя бы один сомножитель будет равен нулю,то уравнение будет равно нулю
х-6=0    х=6      х²+6х+39=0     D=36-4*39<0     корней нет 
ответ:   х=6

Answer 2

x = 6; (x - 6)·(x² + 6x + 39)

Объяснение:

x³ + 3x - 234 = x³ + 3x - 18·13 = x³ + 3x - 18 - 18·12 = x³ - 27·8 + 3·(x - 6) = x³ - (3·2)³ + 3·(x - 6) = (x - 6)(x² + 6x + 36) + 3·(x - 6) = (x - 6)·(x² + 6x + 39);

x = 6 - корень многочлена; второй множитель - квадратный трехчлен с дискриминантом меньше 0, поэтому у него корней нет!

Примечание:

Для того, чтобы не догадываться до разложения многочлена на множители, можно воспользоваться свойством целых (ненулевых) корней целого алгебраического уравнения быть делителем свободного члена и поискать корень среди делителей числа 234:

±1; ±2; ±3; ±6 и т.д. Подойдет число 6. С схемы Горнера можно разделить  x³ + 3x - 234 на x - 6:

$\begin{array}{ccccc}\textbf{6}&1&0&3&-234\\&1&6&39&\textbf{0}\end{array}$

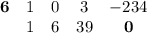
Получаем:

x³ + 3x - 234 = (x - 6)(x² + 6x + 39)

Answer 3

x=6

x³+3·x-234=(x-6)·(x²+6·x+39)

Объяснение:

Дан многочлен x³+3·x-234.

Корнем многочлена P(x) называется число с такое, что P(с)=0.

Поэтому решаем уравнение x³+3·x-234=0.

Из обобщённой теоремы Виета следует, что целые корни уравнения являются делителями свободного члена -234.

Рассмотрим делители числа:

1, 2, 3, 6, 9, 13, 18, 26, 39, 78, 117, 234.

Вычислением можно проверить, что только число 6 является корнем уравнения:

6³+3·6-234=216+18-234=234-234=0.

Тогда

x³+3·x-234=x³-216+3·x-18=x³-6³+3·(x-6)=(x-6)·(x²+6·x+6²)+3·(x-6)=

=(x-6)·(x²+6·x+36+3)=(x-6)·(x²+6·x+39).

Теперь рассмотрим уравнение

x²+6·x+39=0.

Так как D=6²-4·1·39=36-156= -120<0, то квадратное уравнение не имеет решений.

Тогда разложение многочлена имеет вид

x³+3·x-234=(x-6)·(x²+6·x+39).