y = x³ - 4x²
Найдём производную :
y' = (x³)' - 4(x²)' = 3x² - 8x
Найдём критические точки, для этого приравняем производную к нулю.
y' = 0
3x² - 8x = 0
x(3x - 8) = 0
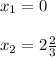
Отметим критические точки на числовой прямой и выясним знаки производной на промежутках, на которые эти точки разбивают числовую прямую .
y'(x) + - +
____________0___________2 2/3_____________
y(x) ↑ ↓ ↑
На промежутках (- ∞ ; 0] и [2 2/3 ; + ∞) -функция возрастает
На промежутке [0 ; 2 2/3] - функция уюывает
Разложим знаменатель на множители:
Сумма коэффициентов равна нулю, значит корни уравнения 1 и -1/3.
Интеграл примет вид:
Разложим дробь, стоящую под знаком интеграла, на составляющие:
Дроби равны, знаменатели равны, значит равны и числители:
Многочлены равны, когда равны коэффициенты при соответствующих степенях. Составим систему:
Выразим из второго уравнения А:
Подставляем в первое и находим В:
Находим А:
Сумма принимает вид:
Значит, интеграл примет вид:
Для второго слагаемого выполним приведение под знак дифференциала:
Интегрируем:
Упрощаем:
Применим свойство логарифмов:
у⁾=(х³-2х²-4)⁾=3х²-4х
у⁾=3х²-4х=0
х(3х-4)=0
х=0 3х-4=0 х=4/3
у(0)=-4
у(4/3)=(4/3)³-2(4/3)²-4=64/27 -32/9 -4= (64-96-108)/27 = -140/27 = -5. 5/27
у⁾⁾=(3х²-4х)⁾=6х-4
у⁾⁾(0)=6*0-4=-4<0 ⇒ точка (0; -4) - точка максимума
у⁾⁾(4/3)=6 *4/3 -4= 4 >0 ⇒точка минимума
ответ : точка максимума (0;-4)