ответ: 12√39 (ед. площади)
Объяснение:
Прямоугольный треугольник с катетами 3 и 4 - египетский, его гипотенуза 5 ( проверьте по т.Пифагора).
Проекция ВС наклонной В1С перпендикулярна СА. По т. о 3-х перпендикулярах В1С⊥СА. Треугольник В1СА - прямоугольный с углом В1АС=60°. В1С=АС•tg60°=4√3. Т.к. призма прямая, боковые ребра перпендикулярны основаниям, поэтому треугольник В1ВС прямоугольный. По т. Пифагора В1В=√(B1C²-BC²)=√[(4√3)²-3²]=√39
Боковое ребро прямой призмы является её высотой, а её боковые грани - прямоугольники.
Площадь боковой поверхности призмы находят умножением её высоты на периметр основания.
S(бок)=В1В•(АВ+ВС+АС)=√39•12=12√39 (ед. площади)

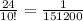

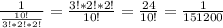
a5=a1+4d=23+16=39
a10=a1+9d=23+36=59
2. a1=3 a2=12
d=a2-a1=12-3=9
S10=(2а1+9d)/2 * 10 = 87*5=435
3. b1=3 b2=-9 b3=27
q=b2/b1=-9/3=-3
b5=b1*q^4=3*81=243
b7=b1*q^6=3*729=2187
4. b1=2 q=4
S7=(b1(q^7 - 1))/(q-1)=(2(4^7 - 1)/3 = 10922
5. a1=-3 d=2
S6=(2a1+5d)/2 * 6=(-6+10)/2 * 6 = 12
S10=(2a1+9d)/2 * 10=(-6+18)/2 *10=60
S10-S6=60-12=48