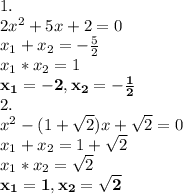
ответ
672, 673, 674
или
1009, 1010
Пояснения
Последовательность натуральных чисел - это арифметическая последовательность
Таким образом
Пусть a₁ - первое число в данной последовательности
Тогда
d = 1
S = ( 2a₁+d(n-1) )n/2 = 2019 = 3*673
(2a₁+n -1)n = 4038 = 6*673 = 2*3*673
Так как a₁, n - целые, то возможны варианты
n = 1, (2a₁) = 4038, a₁ = 2019, последовательность 2019, состоящую из одного члена последовательностью не считаем
n = 2, (2a₁+1)2 = 4038, a₁ = 1009, последовательность 1009, 1010
n = 3, (2a₁+2)3 = 4038, a₁ = 672, последовательность 672, 673, 674
n = 673, (2a₁+672)673 = 4038, a₁ = (6 - 672)/2 не подходит т. к. a1 ≥ 1
n = 1346, (2a₁+1345)1346 = 4038, a₁ = (3 - 1345)/2 не подходит т. к. a1 ≥ 1
n = 2019, (2a₁+2018)2019 = 4038, a₁ = (2 - 2018)/2 не подходит т. к. a1 ≥ 1
n = 2019, (2a₁+4037)4038 = 4038, a₁ = (1 - 4037)/2 не подходит т. к. a1 ≥ 1