ответ: 1-б. 2-а, 3-г, 4-, 5- , 6-в, 7-г
Объяснение:
1. Найдите значение алгебраической дроби 2х/х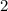
-1, при х= 1/3
• а) 0,75; б) -0,75 ; в) - ;г) -1,5
2. Найдите значение x, при котором дробь х+2/х-4 не имеет смысла
а)4 б)-2 в) -4 г) нет таких значений
3. Какое из предложенных выражений записано в виде алгебраической дроби?
а)2х/3+х ; б)2/х2+3х в)81х2/13-х ; г)2/3-х
4. Найдите значение выражения , при а= -0,7, в=0,3
а)2,5; б) -2,5; в) 1; г) другой ответ.
5.При каком значении а дробь не определена?
а) 0; б) - ; в) ; г)другой ответ.
6. Найди допустимые значения букв, входящих в дробь а/b
а) любые значения; б)5 возможных значений ; в) любые значения а и b, при b не равным 0 ; г) нет ответа
7.Выберите дробно- рациональные выражения 2х/3+4/7, 2-5х/7,3, 3/х-2
а) нет правильного ответа ; б) 2х/3+4/7 ; в)2-5х/7,3 ; г) 3/х-2
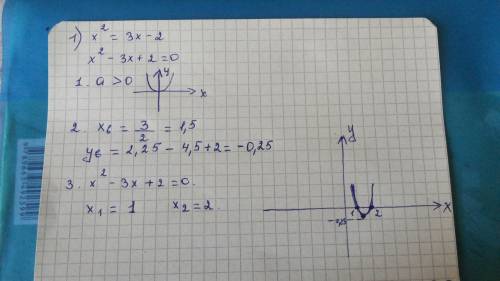
Я полагаю что в задании неточность. Функция должна по здравому смыслу такой:
у = 3х² + 6х + 2
типа у = ах² + вх + с,
где а = 3, в = 6, с = 2
График этой функции квадратна парабола веточками вверх, т.к а > 0.
вершина параболы имеет координаты
Хв = -в/2а = - 6/(2·3) = -1
Ув = 3 - 6 + 2 = -1
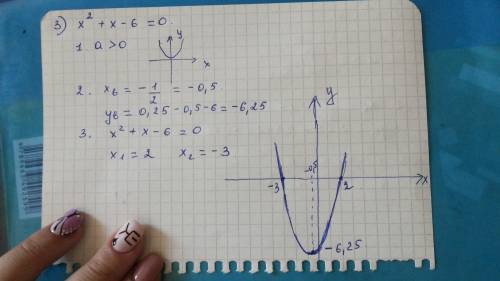
График функции пересекает ось х в точках, где у = 0
3х² + 6х + 2 = 0
D = 36 - 24 = 12
√D = √12 = 2√3 ≈ 3,464
х₁ = (-6 - 3,464):6 = -1,577
х₂ = (-6 + 3,464):6 = -0,423
для таблицы произведём подсчёты
х = 3 у = 3·9 + 6·3 + 2 = 47
х = 2 у = 3·4 + 6·2 + 2 = 26
х = 1 у = 3 + 6 + 2 = 11
х = 0 у = 2
х = -1 у = 3 + -6 + 2 = -1(минимальное значение)
относительно прямой х = -1 график симметричен, поэтому и значения функции в симметричных точках одинаковы
х = -2 у = 2
х = -3 у = 11
х = -4 у = 26
х = -5 у = 47
Составляем таблицу
х 3 2 1 0 -0,423 -1 -1,577 -2 -3 -4 -5
у 47 26 11 2 0 -1 0 2 11 26 47
