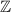Решите систему уравнений. -12+3х> 0 9-4х> -3 ответ: нет решений. как решить это?

👇

Ответ:

maryana070803

01.12.2020

3x>12 ⇒ x>4 то есть для этого неравенства все решения будут больше 4
4x<12 ⇒ x<3 то есть для этого неравенства все решения будут меньше 3
Общих решений для этих неравенств нет

4,4(33 оценок)

Ответ:

Iryna452

01.12.2020

Ваше задание выполнено
Решите систему уравнений. -12+3х> 0 9-4х> -3 ответ: нет решений. как решить это?

4,7(50 оценок)

Открыть все ответы

Ответ:

иринка2807

01.12.2020

Множество целых чисел $\mathbb{Z}$ разделим на три класса:
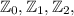$\mathbb{Z} = \mathbb{Z}_0 + \mathbb{Z}_1 + \mathbb{Z}_2$ , где + обозначает операцию объединения и изначает, что множества $\mathbb{Z}_0,\mathbb{Z}_1,\mathbb{Z}_2,$ дисъюнктны.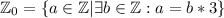
$\mathbb{Z}_0 = \{a \in \mathbb{Z} | \exists{b \in \mathbb{Z}: a = b*3}\}$
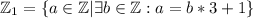
$\mathbb{Z}_1 = \{a \in \mathbb{Z} | \exists{b \in \mathbb{Z}: a = b*3+1}\}$
$\mathbb{Z}_2 = \{a \in \mathbb{Z} | \exists{b \in \mathbb{Z}: a = b*3+2}\}$
Данное разделение множества целых чисел существует по принципу решета Эрастофена.
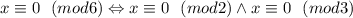
$x \equiv 0\ \ (mod 6) \Leftrightarrow x \equiv 0 \ \ (mod 2) \land x \equiv 0 \ \ (mod3)$
x^3 + 41x = x(x^2 + 41)

.
Так как при четном x выражение делится на два, а при нечетном x^2 + 41

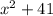делится на два (сумма нечетных чисел четна), то есть выражение все равно делится на два, первое условие выполнено. Докажем, что x делится на 3:
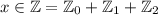Так как $x \in \mathbb{Z} = \mathbb{Z}_0 + \mathbb{Z}_1 + \mathbb{Z}_2$ , то рассмотрим три случая:
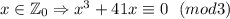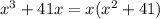1) $x \in \mathbb{Z}_0 \Rightarrow x^3 + 41x \equiv 0 \ \ (mod 3)$ так как x^3 + 41x = x(x^2+41)

.
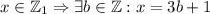
2) $x \in \mathbb{Z}_1 \Rightarrow \exists{b \in \mathbb{Z} : x = 3b + 1}$
x^2 + 41 = (3b)^2 + 2*(3b)*41 + 1 + 41 = 3*m + 42 = 3*n

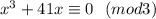для каких-то $m,n \in \mathbb{Z}$ , то есть $x^3+41x \equiv 0 \ \ (mod 3)$ .
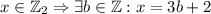3) $x \in \mathbb{Z}_2 \Rightarrow \exists{b \in \mathbb{Z} : x = 3b + 2}$ .
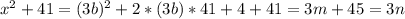x^2 + 41 = (3b)^2 + 2*(3b)*41 + 4 + 41 = 3m + 45 = 3n

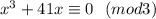для каких-то $m,n \in \mathbb{Z}$ , то есть $x^3+41x \equiv 0 \ \ (mod 3)$ .
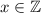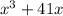Тогда для всех $x \in \mathbb{Z}$ выражение x^3+41x

делится на 6.

4,8(77 оценок)

Ответ:

slipnot174

01.12.2020

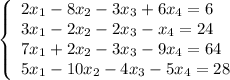
$\left\{\begin{array}{l}2x_1-8x_2-3x_3+6x_4=6\\3x_1-2x_2-2x_3-x_4=24\\7x_1+2x_2-3x_3-9x_4=64\\5x_1-10x_2-4x_3-5x_4=28\end{array}\right$

Для удобства вычислений, поменяем местами строчки системы ЛНУ .

$\left\{\begin{array}{l}5x_1-10x_2-4x_3-5x_4=28\\7x_1+2x_2-3x_3-9x_4=64\\3x_1-2x_2-2x_3-x_4=24\\2x_1-8x_2-3x_3+6x_4=6\end{array}\right\ \ \ \Rightarrow \ \ \ \left(\begin{array}{ccccc}5&-10&-4&-5\ |\ 28\\7&2&-3&-9\ |\ 64\\3&-2&-2&-1\ |\ 24\\2&-8&-3&6\ \ |\ 6\end{array}\right)\sim$

1 строку * 7 - 5*2 строку ; 1стр*3 - 5*3стр ; 1стр*2-5*4стр

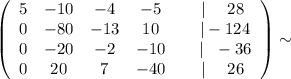
$\left(\begin{array}{ccccc}5&-10&-4&-5\ &\ |\ \ \ \ 28\\0&-80&-13&10\ &\ \ |-124\\0&-20&-2&-10\ &\ \ |\ \ -36\\0&20&7&-40\ &\ |\ \ \ \ 26\end{array}\right)\sim$

2стр - 4*3стр ; 3 стр + 4стр

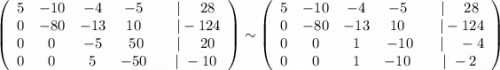
$\left(\begin{array}{ccccc}5&-10&-4&-5\ &\ |\ \ \ \ 28\\0&-80&-13&10\ &\ \ |-124\\0&0&-5&50&\ |\ \ \ \ 20\\0&0&5&-50\ &\ |\ -10\end{array}\right)\sim \left(\begin{array}{ccccc}5&-10&-4&-5\ &\ |\ \ \ \ 28\\0&-80&-13&10\ &\ \ |-124\\0&0&1&-10&\ \ |\ \ \ -4\\0&0&1&-10\ &\ |\ -2\end{array}\right)$

Для перехода к последней матрице разделили 3 строку на (-5) , а 4 строку на 5 .

Ранг матрицы системы ( та, что записана до вертикальной черты, размером 4×4 ), равен 3, так как две последние строки равны, а значит одну из строк можно вычеркнуть. Ранг расширенной матрицы ( та, что записана без учёта вертикальной черты, размером 4×5 ) равен 4, так как2 последние строки различны. Ранги указанных матриц НЕ равны, то есть условия теоремы Кронекера-Капелли не выполняются, значит система НЕ ИМЕЕТ РЕШЕНИЙ, то есть система НЕСОВМЕСТНА .

Общее решение системы можно было бы записать лишь в случае, если бы система была совместна и не определена .