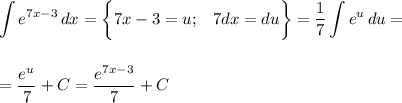
1. Прежде всего, разобьем это выражение на множители:
n^4+2n^3+3n^2+2n=n*(n^3+2n^2+3*n+2)
Разделив столбиком многочлен n^3+2n^2+3*n+2 на (n+1), получаем (n^2+n+2). Т.е. исходный многочлен может быть представлен в следующем виде:
n^4+2n^3+3n^2+2n=n*(n+1)*(n^2+n+2)
2. Теперь рассмотрим 2 случая:
а). Пусть n - четное число, т.е. делится на 2 без остатка, тогда
n делится на 2 без остатка;
(n+1), будучи числом нечетным, не делится на 2 без остатка;
Теперь рассмотрим n^2+n+2:
n - четное, значит n^2 - тоже четное, и n^2+n - тоже четное, т.е. делится на 2 без остатка. Т.к. n^2+n уже делится на 2 без остатка, то n^2+n+2 также еще раз разделится на 2 без остатка => (n^2+n+2)/2=((n^2+n)/2) + 2/2=((n^2+n)/2)+1.
Получаем, что исходное выражение можно три раза разделить на 2, т.е. разделить на 8.
б). Пусть n - нечетное, т.е. не делится на 2 без остатка, тогда
n не делится на 2 без остатка;
(n+1), будучи числом четным, делится на 2 без остатка;
n - нечетное, значит n^2 - тоже нечетное, а n^2+n - уже четное, т.к. к нечетному n^2 прибавляем нечетное n. И аналогично, т.к. n^2+n уже делится на 2 без остатка, то n^2+n+2 также еще раз разделится на 2 без остатка.
Получаем, что исходное выражение можно три раза разделить на 2, т.е. разделить на 8.
Пусть х - искомое число, тогда
(100-х) - первое вновь полученное число
(30+х) - третье вновь полученное число.
По условию произведение вновь полученных чисел равно квадрату второго числа, получаем уравнение:
(100-х)·(30+х) = 60²
3000-30х+100х-х² = 3600
-х²+70х-600 = 0
Делим обе части уравнения на (-1)
х²-70х+600 = 0
D = 4900-4·1·600=4900-2400= 2500 = 50²
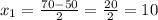
x₁ = 10
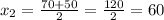
x₂ = 60
1) Проверим х₁=10.
(100-10)·(30+10) = 60²
90 · 40 = 3600
3600 = 3600 верное равенство
2) Проверим x₂=60.
(100-60)·(30+60) = 60²
40 · 90 = 3600
3600 = 3600 верное равенство
ответ: 10; 60