1)2(3x+7)-8(x+3)<_3
6x"+14 - 8x -24 -3 <_0
-2x<_13
x>_ - 6,5 отмечаем на координатной прямой ,точка будет выколотой и [ -6,5. +бесконечность)
2)-3x^2 +8x + 3=0
D = 64- 4*(-3)*3= 64+ 36=100=10^2
x1= -8 +10 / -6 = -2/6=-1/3
x2=-8 - 10 /-6 = 3
OTVET : -1/3 ; 3
3)4x^2 - 4x - 15 <0
D= 16-4*4*(-15) = 16+ 240= 256= 16^2
x1= 4+16 / 8= 20/8=5/4
x2=4-16/ 8= -12/16 = -3/4
4)8+2x-6 = 4x+7
-2x = 5
x=-2,5
5) 5x +4 _> 2
3-2x <_ 4
5x _> -2
-2x<_1
x_>-2/5
x>_-1/2
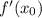производная функции в данной точке. А 
точка касания по иксу.
мы должны найти производную общего типа этой функции.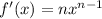
- где n это степень.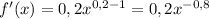
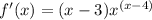
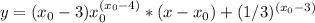
и получаешь уравнение касательной.
Так как коэффициент, стоящий при x^2, больше нуля(в твоём случае он равен 5), то ветви направлены вверх.