график ф-ии будет задан формулой y=(x+4)(x^2-4x+4)-22
y = x^3-4x^2+4x+4x^2-16x+16-22
y = x^3 - 12x - 6
несомненно, что это кубическая парабола, найдем ее точки перегиба
y' = 3x^2 - 12 = 0 решив это уравнение получаем, что точки перегиба в точках x=-2 и х=2
найдем значения ф-ии в точках перегиба и на концах отрезка
x=-4 y=-22
x=-2 y=10
x=2 y=-22
x=3 y=-15
максимальное значение ф-ии в точке х=-2 равное 10
ответ 10
но проще всего просто написать программку, которая перебирает значение с шагом в 1/1000 по всему заданному приоду и выводит максимум и минимум
Пусть нужно сложить почленно два многочлена:
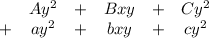
Как можно поступить? Можно непосредственно писать, что сумма равна
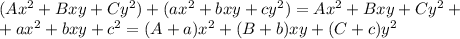
А можно сразу "приводить подобные" и складывать только коэффициенты. Тогда результат получится быстрее.
Тоже самое можно делать и с уравнениями. Пусть нужно почленно сложить 2 равенства:
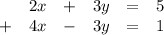
Складываем правые и левые части равенств точно так же, как и обычные многочлены. Тогда слева будет (2+4)х+(3-3)у,. а справа 5+1. Получившееся уравнение простое: 6х=6. Так, без использования подстановок можно решать или упрощать системы уравнений.
б) имеет
В) не имеет по той же причине, что и в а)
г) имеет