Графиком линейной функции является прямая.
х - независимая переменная, то есть может принимать любые значения.
у - зависимая переменная, то есть её значение зависит от значения х.
Чтобы построить график, возьмём две точки.
Если х = 0, у = 2
Если х = 1, у = 3
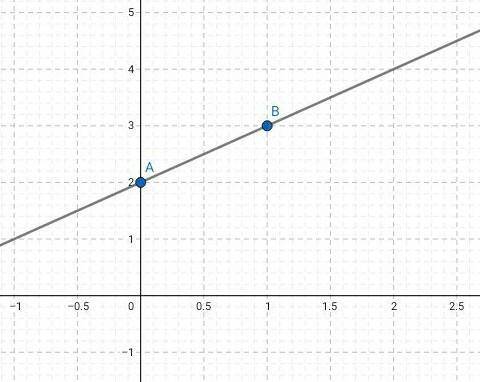
У нас есть координаты двух точек А (0;2), В (1;3). Теперь, построим график:
Задание#2А) Если х = 3 то у = 3 + 2 = 5
ответ: у = 5
Б) Если у = 0, то х:
0 = х + 2
-х = 2
х = -2
ответ: х = -2
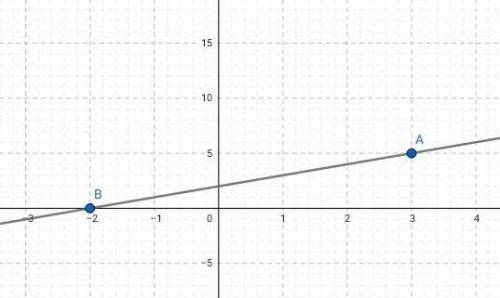
Если нужен график точек А (3;5) и В (-2;0), то он тоже прикреплен 2 картинкой.
1)Решение системы уравнений (6; 1);
2)Решение системы уравнений (4; -1).
Объяснение:
1)Решить систему уравнений методом подстановки:
х-у=5
4х-у=23
Выразим х через у в первом уравнении, подставим выражение во второе уравнение и вычислим у:
х=5+у
4(5+у)-у=23
20+4у-у=23
3у=23-20
3у=3
у=1
х=5+у
х=5+1
х=6
Решение системы уравнений (6; 1)
2)Решить систему уравнений методом сложения:
2х+3у=5
15х+6у=54
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.
В данной системе нужно первое уравнение умножить на -2:
-4х-6у= -10
15х+6у=54
Складываем уравнения:
-4х+15х-6у+6у= -10+54
11х=44
х=4
Теперь подставляем значение х в любое из двух уравнений системы и вычисляем у:
2х+3у=5
3у=5-2х
3у=5-2*4
3у= -3
у= -1
Решение системы уравнений (4; -1)
Обозначим гипотенузу за х.
И строим чертеж.
Вторая математическая модель будет составление формулы.
Воспользуемся теоремой Пифагора.
AB²=AC²+CB² (Для нахождения сторон)
S=0.5*AC*CB (Для нахождения площади)
Третья математическая модель - решение.
x²=(x-9)²+(x-8)²
x²=x²-18x+81+x²-16x+64
x²-34x+145=0
D=289-145=144
x₁=17+12=29
x₂=17-12=5
Проверим
АС=5-9=-4 (Сторона не может быть отрицательной)
AC=29-9=20 (дм)
CB=29-8=21 (дм)
AB=29 (дм)
S=0.5*20*21=210 (дм²)