sin (5πx/9) = sin (πx/9) + sin (2πx/9)
sin (5πx/9) - sin (πx/9) = sin (2πx/9)
По формуле разности синусов:
2sin(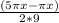
)cos(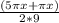
) - sin (2πx/9) = 0;
2 sin(2πx/9)cos(πx/3) - sin(2πx/9)=0;
sin (2πx/9) (2cos(πx/3)-1)=0;
sin (2πx/9)=0 или 2cos (πx/3)=1; cos (πx/3)=1/2
2πx/9=πn, n∈Z или πx/3=π/3+2πn, n∈Z или πx/3=-π/3+2πn, n∈Z;
Сокращаем на π:
2x/9=n, n∈Z или x/3=1/3+2n, n∈Z или x/3=-1/3+2n, n∈Z;
x=9n/2 или x=6n+1 или x=6n-1
Теперь отбираем корни уравнения, принадлежащие промежутку (4;8)
4<(9/2)n<8; 8/9<n<16/9; n=1, x=4,5
4<6n+1<8; 3<6n<7; 1/2<n<7/6; n=1; x=6+1=7;
4<6n-1<8; 5<6n<9; 5/6<n<3/2; n=1; x=6-1=5
ответ: x={4,5;5;7}
b₂ *b₄ = 144, подставим. получим:(30 - b₄)*b₄ = 144, ⇒30b₄- b₄² = 144,⇒
S₉ - ?
⇒ b₄² -30b₄ +144 = 0 по т. Виета а)b₄ = 6 и б)b₄ = 24
b₂= 24 b₂ = 6
подходит 2-й вариант
b₂= 6
b₄=24
b₃=12, значит, q = 2, a b₁=3
S₉ = b₁(b⁹ -1)(q -1) = 3(512-1)/1 = 3*511 = 1533