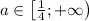а) Рассмотрим уравнение 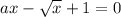 (a=0 подходит тогда х=1)сделаем замену переменных
(a=0 подходит тогда х=1)сделаем замену переменных 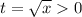 . Получим уравнение
. Получим уравнение
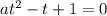 (здесь
(здесь 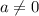 )Данное квадратное уравнение имеет 1 корень, если дискриминант D=0. Однако, если уравнение имеет 2 решения, причем разного знака, то нам подходит только одно положительное. Следовательно, в этом случае исходное уравнение будет иметь тоже 1 корень. Поэтому рассматриваем случай, когда
)Данное квадратное уравнение имеет 1 корень, если дискриминант D=0. Однако, если уравнение имеет 2 решения, причем разного знака, то нам подходит только одно положительное. Следовательно, в этом случае исходное уравнение будет иметь тоже 1 корень. Поэтому рассматриваем случай, когда 
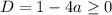 Тогда
Тогда 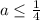
Далее пусть меньший корень будет < 0, а больший >0.
Необходимо рассмотреть 3 случая:
1) 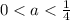
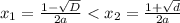
 Тогда D>1, следовательно a<0. Получаем нет решений.
Тогда D>1, следовательно a<0. Получаем нет решений.
2) 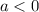
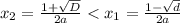
 Тогда
Тогда 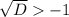 всегда выполняется.
всегда выполняется.
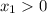 Тогда D>1, следовательно a<0.
Тогда D>1, следовательно a<0.
3) 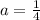
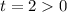
Таким образом 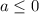 и
и 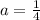
б) неравенство 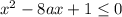 будет иметь хотя бы один решение, если
будет иметь хотя бы один решение, если 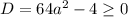 . Отсюда получаем a из
. Отсюда получаем a из ![(-\infty ; -\frac{1}{4}]\cup{[\frac{1}{4};+\infty)}](/tpl/images/0040/0927/4f9da.png)
а)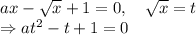 .
.
Это квадратное уравнение имеет один корень, если его дискриминант равен нулю, т.е.
б)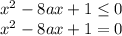
Это квадратное уравнение имеет хотя бы один корень, если дискриминант неотрицателен, т.е.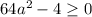 . Это неравенство справедливо при
. Это неравенство справедливо при