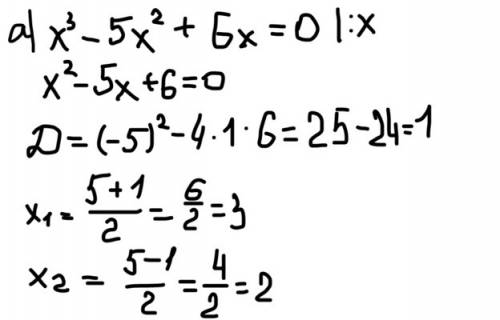
Объяснение:
1. Найдите гипотенузу, если катеты равны 2см и 5 см
по теореме Пифагора гипотенуза равна
√(2²+5²)=√29 см
2. Найдите катет, если гипотенуза равна 8см, а второй катет равен 3см
по теореме Пифагора катет равен √(8²-3²)=√(64-9)=√55 см
3. Найдите сторону ромба, если его диагонали равны 6 см и 8
Диагонали в точке пересечения делятся пополам и половинки диагоналей образуют со стороной ромба прямоугольный треугольник в котором сторона является гипотенузой и равна
по теореме Пифагора гипотенуза равна
√(6²+8²)=√100=10 см
В решении.
Объяснение:
Построить графики функций и найти её область определения.
Область определения - это проекция графика функции на ось Ох, это значения х, при которых функция существует.
Обозначается как D(f) или D(у).
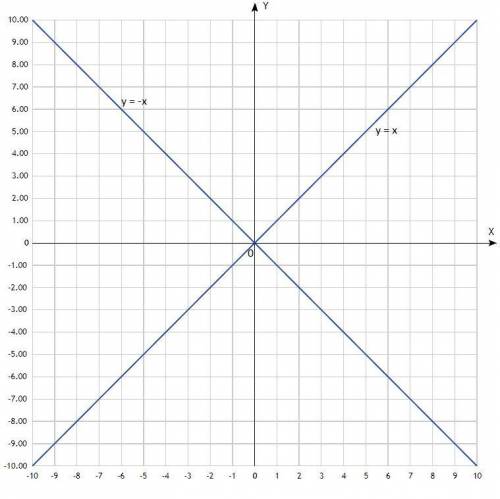
1) у = х;
Таблица:
х -1 0 1
у -1 0 1
График - прямая линия, проходящая через начало координат, ничем не ограничена, х может быть любым.
D(у) = х∈R;
2) у = -х;
Таблица:
х -1 0 1
у 1 0 -1
График - прямая линия, проходящая через начало координат, ничем не ограничена, х может быть любым.
D(у) = х∈R;
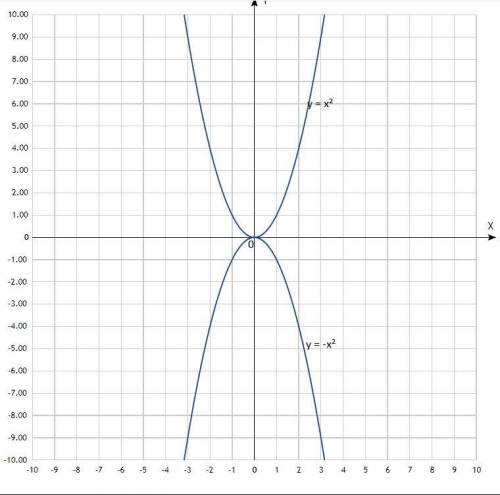
3) у = х²
График - классическая парабола с вершиной в начале координат, ветви направлены вверх.
Таблица:
х -3 -2 -1 0 1 2 3
у 9 4 1 0 1 4 9
Область определения параболы - множество всех действительных чисел, потому что она проецируется на любую точку оси Ох.
D(у) = х∈R;
4) у = -х²
График - классическая парабола с вершиной в начале координат, ветви направлены вниз.
Таблица:
х -3 -2 -1 0 1 2 3
у -9 -4 -1 0 -1 -4 -9
Область определения параболы - множество всех действительных чисел, потому что она проецируется на любую точку оси Ох.
D(у) = х∈R;
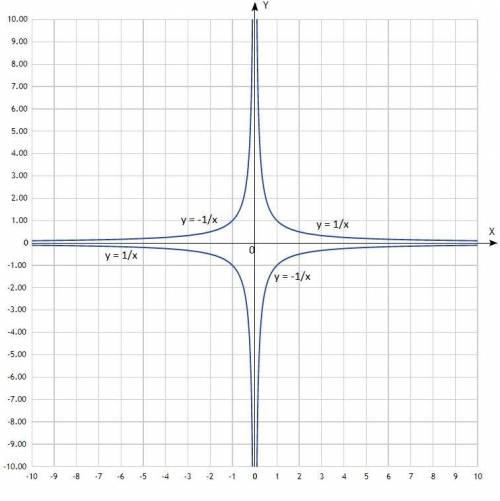
5) у = 1/х
График - гипербола, расположена в 1 и 3 координатных четвертях.
Таблица:
х -10 -5 -1 0 1 5 10
у -0,1 -0,2 -1 - 1 0,2 0,1
Область определения - множество всех действительных чисел, кроме х = 0 (на ноль делить нельзя).
D(у) = х∈R : х ≠ 0;
6) у = -1/х
График - гипербола, расположена во 2 и 4 координатных четвертях.
Таблица:
х -10 -5 -1 0 1 5 10
у 0,1 0,2 1 - -1 -0,2 -0,1
Область определения - множество всех действительных чисел, кроме х = 0 (на ноль делить нельзя).
D(у) = х∈R : х ≠ 0;
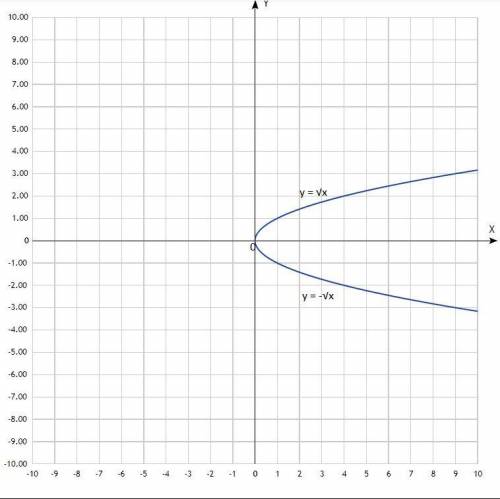
7) у = √х
Графиком функции y=√x является ветвь параболы.
Таблица:
х 0 1 4 9
у 0 1 2 3
Область определения - множество всех действительных чисел, только х больше либо равен нулю.
D(у) = х∈R : х >= 0;
8) у = -√х
Графиком функции y = -√x является ветвь параболы.
Таблица:
х 0 1 4 9
у 0 -1 -2 -3
Область определения - множество всех действительных чисел, только х больше либо равен нулю.
D(у) = х∈R : х >= 0;
1) x^2+3.5x-2=0
2x^2+7-4=0
D=49+32=81=9^2
X=-4;0.5
ответ: -4; 0.5
2) x^2-6x+24-4x+1=0
x^2-10x+25=0
D=100-100=0
x=3
ответ: 3
3) 2x^2-7x+9
D=49-72
Пустое множество
4) 7+2(x-4) x+4
2x=1 x=-4
x=0.5 > x=-4
от - бесконечности до 0.5 и от 4 до плюс бесконечности все включительно
5) -0.4x+0.6 6x+1.5
x=-1.5 < x=-0.25
от -1.5 до 0.25 все не включительно
6) -3x-6+2x-2 3x-9+2
-x=8 3x=7
x=8 > x=3.5
от - бесконечности до 3.5 и от 8 до плюс бесконечности все не включительно
д) x+1+2x+2+3x-3 4x+3x-6
6x=0 7x=6
x=0 < x=6/7
от 0 до 6/7 все не включительно
г) x-1/3+7x-7 4x+2
-6x=22/3 x=-0.5
6x=-22/3 < x=-0.5
от (-22/3)/6 до -0.5 все включительно