

Объяснение: 

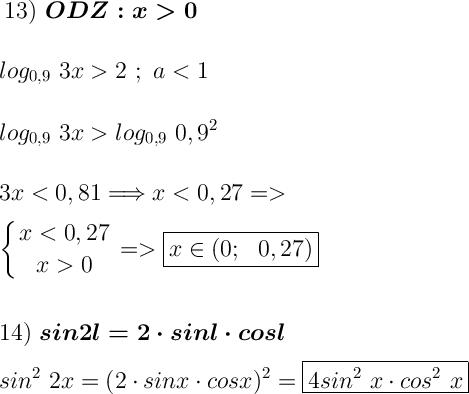

Доказательство:
Дана последовательность
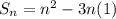
Допустим, что эта последовательность арифметическая прогрессия, тогда
при n = 1 получаем

при n = 2

и
а₂ = -2 - а₁ = -2 + 2 = 0
Таким образом разность арифметической прогрессии
d = a₂ - a₁ = 0 + 2 = 2
По известной формуле найдем n-й член арифметической прогрессии
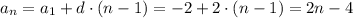
Известно, что сумма n членов арифметической прогрессии
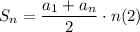
Докажем, что выражение (2) тождественно выражению (1) при
a₁ = -2 и 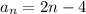 , подставив в (2)
, подставив в (2)
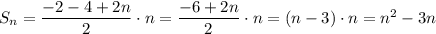
Тождество доказано.
Следовательно, последовательность, определённая суммой 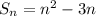 является арифметической прогрессией.
является арифметической прогрессией.