Объяснение:
P = 28 м - периметр прямоугольника
P = 2 (a+b) - периметр прямоугольника, где a и b -стороны
a+b = P:2
a+b = 28:2 = 14 м
a = 14-b
S = 40 м² - площадь прямоугольника
S = a*b - площадь прямоугольника, где a и b -стороны
40 = a*b
40 = (14-b)*b
40 = 14b - b²
b²-14b+40 = 0
Решим квадратное уравнение
D = b² - 4ac = (-14)² - 4*1*40 = 36
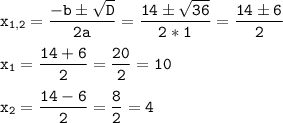
Корнями уравнений являются значения 4 и 10, значит сторона b может быть равна либо 4 м, либо 10 м.
b₁ = 4 м, b₂ = 10 м
Найдем сторону a
a = 14-b
a₁ = 14-b₁ = 14-4 = 10 м
a₂ = 14-b₂ = 14-10 = 4 м
ответ: a = 10 м, b = 4 м, или a = 4 м, b = 10 м.
у=-1*0-7.45 = -7.45
(0; - 7.45)-координаты вершины параболы