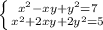
Сложим первое уравнение,домноженное на 2 со вторым:
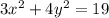
Очевидно,что x и y не обращаются в ноль,так как число 19 простое и не имеет делителей на интервале (1;19)
Значит:
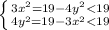
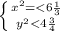
![\left \{ {{|x| \in [1;2]} \atop {|y| \in [1;2]}} \right](/tpl/images/0099/8562/6984c.png)
Из полученных отрезков лишь пара значений модулей удовлетворяет нашему уравнению:
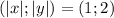
Осталось лишь раскрыть модуль,сделаем это следующим образом:
Рассмотрим полиномы вида:
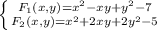
Подставим модули корней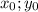 
под степени 2,так как они являются четными и не меняют значение:
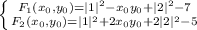
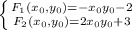
Очевидно,что для старших мономов вида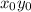 
обоих полиномов для обращения последних в ноль определен отрицательный знак.Это выполнимо в случае только одного отрицательного и одного положительного переменного.
Значит возможные целочисленные значения решения исходной системы:
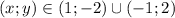
1)Для нахождения члена арифмитической прогрессии надо воспользоваться формулой An=A1+(n-1)*d n=25 d=-0.4 A1=17,6
А25=17,6+ (25-1)*(-0,4)=17,6+24*(-0,4)=17,6-9,6=8
2)В арифмитической прогрессии каждый следущий член увеличивается или уменьшается на одно и то же число.Поэтому мы проверяем прогресию под буквой а
первый член 1 второй 4 между ними разница 3 (4-1=3) проверяем дальше 7-4=3 10-7=3 13-10=3 следовательно это арифмитическая прогрессия
проверяем аналогично прогрессию под буквой б
0-3=-3 ;-3-0=-3 ;-6-(-3)=-3; -9-(-6)=-3 следовательно это тоже арифмитическая прогрессия
прогрессия под буквой в
9-4=5;16-9=7
5 не равно 7 следовательно это не арифмитическая прогресия
То есть ответ буквы а и б
А) (у^2-2а)(2а+у^2) = y^4 -4a^2
(a+b)^2 = a^2 +2ab +b^2
Б) (3х^2+х)^2 = 9x^4 +6x^3 +x^2
(a -b)^2 = a^2 -2ab +b^2
В) (2+m)^2(2-m)^2 =( (2+m)(2-m) )^2 = ( 4-m^2 )^2 = 16 -8m^2 -m^4