Для решения запишем формулу бинома Ньютона:
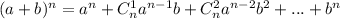
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение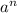 
.
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение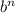 
.
Рассмотрим многочлен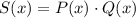 
, где:
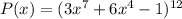
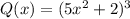
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена :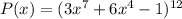
- степень определяется выражением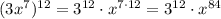 
, то есть степень равна 84
- свободный член равен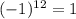 
Для многочлена :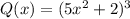
- степень определяется выражением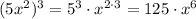 
, то есть степень равна 6
- свободный член равен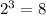 
Наконец, для многочлена 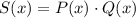получим:
- степень определяется выражением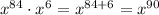 
, то есть степень равна 90
- свободный член равен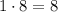 
Сумма степени и свободного члена многочлена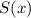 
:
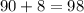
ответ: 98
ответ: x = 14.
Объяснение: одно дело "выразить икс" и совсем другое - решить уравнение)) можно найти икс, постепенно выполняя обратные действия (не раскрывая скобок):
1) делимое = произведению делителя и частного: 1.2*(12_2/3) = (6/5)*(38/3) = 76/5
2) слагаемое = разности суммы и другого слагаемого: (76/5)-6.2 = (76/5)-(31/5) = 45/5 = 9
3) чтобы найти делитель (это самая внутренняя скобка), нужно делимое разделить на частное:
(3_9/16):9 = (57/16)*(1/9) = (19/16)*(1/3) = 19/48
4) уменьшаемое = разность + вычитаемое: (19/48)+(7/24) = (19+14)/48 = 33/48 = 11/16
5) 2.75:(11/16) = (11/4)*(16/11) = 4
получили: х:(2/7) - 45 = 4
x:(2/7) = 45+4=49
x = 49*(2/7) = 14
и всегда полезно делать проверку:
14:(2/7) = 14*7/2 = 7*7 = 49
49-45 = 4
(2.75)/4 = (11/4)*(1/4) = 11/16
(11/16)-(7/24) = (33-14)/48 = 19/48
(3_9/16):(19/48) = (57/16)*(48/19) = 3*3 = 9
9+6.2 = 15.2
(15.2):(12_2/3) = (76/5)*(3/38) = 6/5 = 12/10 = 1.2
а выразить икс гораздо сложнее...
Пусть х синих шаров-число благоприятных вариантов.
Тогда число всех вариантов 4+5+х=9+х.
Составим уравнение:
Находим общее количество шаров в ящике: 4+5+3=12 шаров.
ответ: 12.