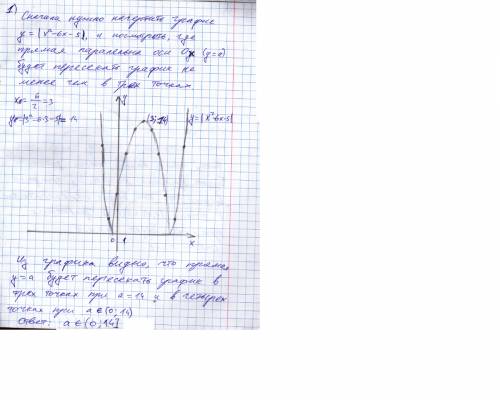
1) квадратное уравнение с модулем будет иметь не менее трех корней если прямая а проходит через вершину параболы -(x^2-6x-5) - это верхнее значение параметра,
а нижнее а=0.
находим вершину параболы, х0=-b/2a у нам b=6 a=-1 x0=3
y0=-9+5+18=14
значит а [0;14]
2) sqrt(x-1)=a+x x>=1
x-1=x^2+a^2+2ax
x^2+(2a-1)x+a^2+1=0
D>0 (2a-1)^2-4a^2-4>0 -4a-3>0 a<-3/4
3) 4x^2-15x+4a^3=0
x1=x2^2
x1*x2=a^3
x2^3=a^3 x2=a
15/4=x1+x2 15/4=a^2+a
4a^2+4a-15=0 a1=3/2 a2=-5/2
x^2-ax+(a-1)=0
x1^2+x2^2=(x1+x2)^2-2x1x2=17
a^2-2(a-1)=17
a^2-2a-15=0
a1=5 a2=-3



xy(3-xy)=2, обозначим t=xy, тогда t^2-3t+2=0, корни: t1=1, t2=2.
1) xy=1, в 1-м уравнении добавим ху, получим:
x^2+2xy+y^2=3+1, или (x+y)^2=4, отсюда x+y=2 или -2.
В 1-м ур-нии отнимем 3у, получим x^2-2xy+y^2=3-3,
или (x-y)^2=0, отсюда x-y=0, или y=x, и тогда 2x=2 или -2.
Аналогично, при ху=2:
2) xy=2, x^2+2xy+y^2=3+2, (x+y)^2=5,...вродебы так решел)