В решении.
Объяснение:
Решить системы уравнений:
1)8у-х=4
2х-21у=2
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
-х=4-8у
х=8у-4
2(8у-4)-21у=2
16у-8-21у=2
-5у=10
у=10/-5
у= -2;
х=8у-4
х=8*(-2)-4
х= -20.
Решение системы уравнений (-20; -2).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.
2)2х-у=0,5
8х-5у=13
Выразить у через х в первом уравнении, подставить выражение во второе уравнение и вычислить х:
-у=0,5-2х
у=2х-0,5
8х-5(2х-0,5)=13
8х-10х+2,5=13
-2х=10,5
х=10,5/-2
х= -5,25;
у=2х-0,5
у=2*(-5,25)-0,5
у= -10,5-0,5
у= -11;
Решение системы уравнений (-5,25; -11).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.
3)4u+3v=14
5u-3v=25
Разделить первое уравнение на 4 для упрощения:
u+0,75v=3,5
5u-3v=25
Выразить u через v в первом уравнении, подставить выражение во второе уравнение и вычислить v:
u=3,5-0,75v
5(3,5-0,75v)-3v=25
17,5-3,75v-3v=25
-6,75v=7,5
v=7,5/-6,5 (нацело не делится)
v=7 и 5/10 : (-6 и 3/4)
Перевести дроби в неправильные:
v=75/10 : (-27/4)
v= -(75*4)/(10*27)
v= -10/9;
u=3,5-0,75v
u=3,5-0,75*(-10/9)
u=3 и 1/2-3/4*(-10/9)
u=3 и 1/2 + 5/6
u=4 и 1/3
u=13/3.
Решение системы уравнений (-10/9; 13/3).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.
4)10p+7q= -2
2p-22=5q
Разделить первое уравнение на 10 для упрощения:
p+0,7q= -0,2
2p-22=5q
Выразить p через q в первом уравнении, подставить выражение во второе уравнение и вычислить q:
p= -0,2-0,7q
2(-0,2-0,7q)-22=5q
-0,4-1,4q-22=5q
-1,4q-5q=22,4
-6,4q=22,4
q=22,4/-6,4
q= -3,5;
p= -0,2-0,7q
p= -0,2-0,7*(-3,5)
p= -0,2+2,45
p= 2,25.
Решение системы уравнений (2,25; -3,5).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.
Возьмем ваше же уравнение
lx+2l+lxl+lx-2l=4
Левую и правую части уравнения рассматриваем как функции.
f(x)=lx+2l+lxl+lx-2l и g(x)=4
С g(x) все понятно. Это прямая y=4, параллельна Ox.
С f(x) разбираемся. Это кусочная функция. Найдем нули подмодульных выражений:
x+2=0 ⇒ x=-2, x-2=0 ⇒ x=2, x=0.
Имеем интервалы (-∞; -2); [-2; 0); [0; 2); [2; +∞). Запишем равносильный переход:
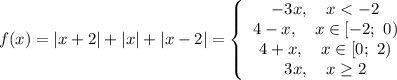
Построение графика на этом этапе элементарно. Из системы можно видеть, что функция f(x) четная. Достаточно построить или левую или правую ее часть, остальное отзеркалить. Готовый рисунок приложен.
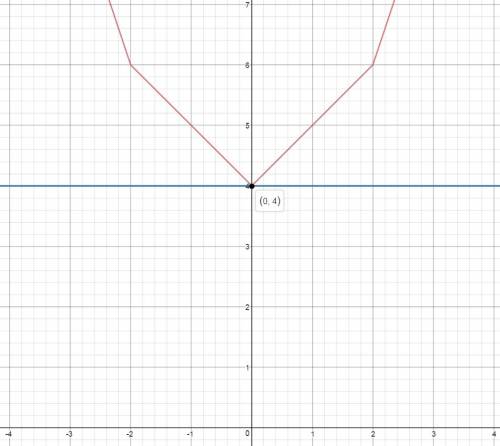
а2=4у=a1+d=50+d
а3=3z=a1+2d=50+2d
a4=2•1=2=а1+3d
а1+3d=2
50+3d=2
3d=–48
d=–16
a2=50–16=34
a3=50–32=18
z=18:3=6
ответ: z=6