1)область визначення множина дійсних чисел (симетрична відносно початку координат)
y(-x)=5(-х)²+1=5х²+1=y(x) - значить дана функція парна за означенням парної функції
2) область визначення множина дійсних чисел (симетрична відносно початку координат)
y(-x)=(-х)⁵+3(-х)³-(-х)=-х⁵-3х³+х=-(х⁵+3х³-х)=-y(x) значить дана функція непарна за означенням непарної функції
3) область визначення множина дійсних чисел (симетрична відносно початку координат)
y(1)=2*1⁴-1³+1=2-1+1=2
y(-1)=2*(-1)⁴-(-1)³+1=2+1+1=4
y(1)не дорівнює y(-1), значить функція не є парною
y(1) не дорівнює -y(-1), значить функція не є не парною
значить дана функція ні парна, ні непарна
4) область визначення множина дійсних чисел, за виключенням точки 0 (симетрична відносно початку координат)
y(-x)=3(-х)-2/(-х)=-3x+2/x=-(3x-2/x)=-y(x) значить дана функція непарна за означенням непарної функції
5) область визначення множина дійсних чисел (симетрична відносно початку координат)
y(1)=4*1²+[1]=4+1=5
y(-1)=4(-1)²+[-1]=4-1=3
y(1)не дорівнює y(-1), значить функція не є парною
y(1) не дорівнює -y(-1), значить функція не є не парною
значить дана функція ні парна, ні непарна
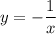и затем верхнюю часть графика отобразить в нижнюю(отрицательную часть)
(*)
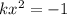и это уравнение решений не имеет при k>0(так как левая часть всегда положительно).
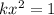и при k<0 это уравнение решений не имеет.
, имеем
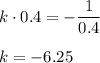
Удачи