Дана функция y = x² + 2 + 6x
Перепишем ее в более удобном виде:
y = x² + 6x + 2
1. Для квадратного уравнения воспользуемся шаблоном:
ax² + bx + c = 0
Найдем коэффициенты:
a = 1;
b = 6;
c = 2;
2. Определим вершины по заданной формуле:

Подставим значения, найденные в пункте:
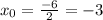
Подставим в изначальную формулу и найдём координату y вершины:
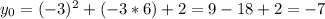
Запишем полученные данные
(-3; -7);
3.
Подставим значения в формулу:
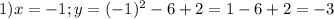
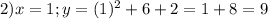
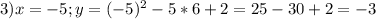

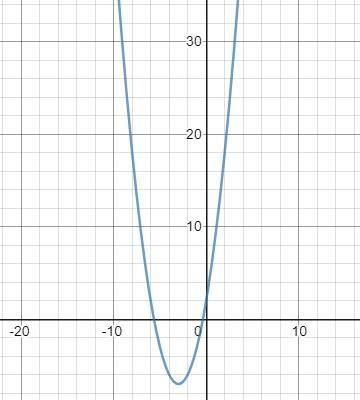
4. (График в прикрепленном файле)
5. Подставим значения:
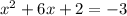
Перенесем "-3":
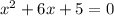
Решим квадратное уравнение:
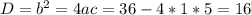
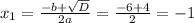
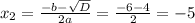
6. По графику функции видно, что наибольшее значение на этом значении при x = 0, а наименьшее это вершина:
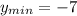
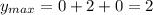
7. С обозначения параболы выплывает, что участок возрастания это все после вершины, а участок убывания до. Тогда:
Возрастания : (-3; +∞)
Убывания: (-∞; -3)
1. Б
Объяснение: Для умножения многочлена на многочлен существует очень легкое правило. Чтобы умножить два многочлена между собой, надо каждый член первого многочлена умножить на каждый член второго многочлена. После это полученные произведения сложить и привести подобные.
2. А
Объяснение: У вырази a*b е два множники, ''a''*b називається першим множником, а*''b'' називається другим множником.
3. В
Объяснение: Спрощуючи даний вираз, згрупуємо окремо числові та буквені множники.
4. Г
5. Б
Объснение: Коэффицие́нт «совместно» + «производящий») — термин, обозначающий числовой множитель при буквенном выражении, множитель при той или иной степени неизвестного, или постоянный множитель при переменной величине.
6. А
-9<x<-4 -9-6<x-y<-4-12
6<y<8 -15<x-y<-16
-9+6<x+y<-4+8
-3<x+y<4