 сумма количества цифр: 1 + 2 = 3 , количество цифр у квадрата числа вдвое больше количества цифр исходного числа.
сумма количества цифр: 1 + 2 = 3 , количество цифр у квадрата числа вдвое больше количества цифр исходного числа. искомая сумма: 1 + 2 = 3 , количество цифр у квадрата числа всё так же вдвое больше количества цифр исходного.
искомая сумма: 1 + 2 = 3 , количество цифр у квадрата числа всё так же вдвое больше количества цифр исходного.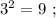 искомая сумма: 1 + 1 = 2 , количество цифр у квадрата равно количеству цифр исходного.
искомая сумма: 1 + 1 = 2 , количество цифр у квадрата равно количеству цифр исходного.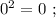 искомая сумма: 1 + 1 = 2 , количество у квадрата равно количеству цифр исходного.
искомая сумма: 1 + 1 = 2 , количество у квадрата равно количеству цифр исходного.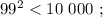 сумма: 2 + 4 = 6 , количество цифр у квадрата вдвое больше количества цифр исходного.
сумма: 2 + 4 = 6 , количество цифр у квадрата вдвое больше количества цифр исходного.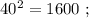 сумма: 2 + 4 = 6 , цифр у квадрата всё так же вдвое больше количества цифр исходного.
сумма: 2 + 4 = 6 , цифр у квадрата всё так же вдвое больше количества цифр исходного.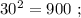 сумма: 2 + 3 = 5 , цифр у квадрата числа: 3 = 4–1 .
сумма: 2 + 3 = 5 , цифр у квадрата числа: 3 = 4–1 . сумма: 2 + 3 = 5 , цифр у квадрата: 3 = 4–1 .
сумма: 2 + 3 = 5 , цифр у квадрата: 3 = 4–1 . сумма: 3 + 6 = 9 , цифр у квадрата вдвое больше.
сумма: 3 + 6 = 9 , цифр у квадрата вдвое больше.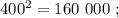 сумма: 3 + 6 = 9 , цифр у квадрата вдвое больше.
сумма: 3 + 6 = 9 , цифр у квадрата вдвое больше.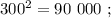 сумма: 3 + 5 = 8 , цифр у квадрата числа: 5 = 3*2–1 .
сумма: 3 + 5 = 8 , цифр у квадрата числа: 5 = 3*2–1 . сумма: 3 + 5 = 8 , цифр у квадрата числа: 5 = 3*2–1 .
сумма: 3 + 5 = 8 , цифр у квадрата числа: 5 = 3*2–1 . сумма: 4 + 8 = 12 , у квадрата вдвое больше.
сумма: 4 + 8 = 12 , у квадрата вдвое больше. сумма: 4 + 8 = 12 , у квадрата вдвое больше.
сумма: 4 + 8 = 12 , у квадрата вдвое больше. сумма: 4 + 7 = 11 , цифр у квадрата: 7 = 4*2–1 .
сумма: 4 + 7 = 11 , цифр у квадрата: 7 = 4*2–1 .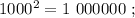 сумма: 4 + 7 = 11 , цифр у квадрата: 7 = 4*2–1 .
сумма: 4 + 7 = 11 , цифр у квадрата: 7 = 4*2–1 .
3x-2y=7
Получаем:
{4x+2y=14
3x-2y=7
7x + 0y = 21
7x=21
x=21:7
x=3
2) подставляем в ЛЮБОЕ НАЧАЛЬНОЕ УРАВНЕНИЕ:
Например: 2x+y=7
2*3 + y=7
6+y=7
=> y= 7/6 или 1.1/6
2)
{3x+4y=-1 Тут всё нужно умножить на -2, чтобы потом избавиться от x
2x+5y=4 Тут всё нужно умножить на 3, чтобы потом избавиться от X
АНАЛОГИЧНО ПЕРВОМУ:
{-6x-8y=2
6x+15y=12
0x+7y=14
7y=14
y=2
2) подставляем в ЛЮБОЕ НАЧАЛЬНОЕ УРАВНЕНИЕ:
Например:
2x+5y=4
2x+5*2=4
2x+10=4
2x=4-10
2x=-6
x= - 3