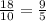1.Решите неравенство методом интервалов
-х(в квадрате)-12х<0
-x^2-12x<0
-x(x-12)<0
x(x-12)>0
ищем критические точки х=0 - первая точка, х-12=0, х=12 - вторая точка
+ - +
012>x
x=13: x(x-12)=13*(13-12)>0
значитна промежутке (12;+бесконечность) л.ч. неравенства больше 0
при переходе через точку 12, меняем знак с + на -, и получаем, что на промежутке (0;12) л.ч. неравенства меньше 0
при переходе через точку 0 меняем знак с - на + ,и получаем, что на промежутке
(-бесконечность; 0) л.ч неравенства больше 0,
таким образом решением неравенства будет
(-бесконечность; 0)обьединение(12;+бесконечность)
2.При каких значениях параметра m уравнение
4х(в квадрате)-2mx+9=0
имеет два различных корня?
уравнение имеет два различных корня если дискриминант больше 0, т.е.
D=(-2m)^2-4*4*9=4m^2-144>0
4(m^2-36)>0
m^2-36>0
(m-6)(m+6)>0
ищем критические точки m+6=0, m=-6 - первая точка, m-6=0, m=6 - вторая точка(-6<6)
+ - +
(-6)6>m
x=7: (m-6)(m+6)=(7-6)(7+6)>0
значитна промежутке (6;+бесконечность) л.ч. неравенства больше 0
при переходе через точку 6, меняем знак с + на -, и получаем, что на промежутке (-6;6) л.ч. неравенства меньше 0
при переходе через точку -6 меняем знак с - на + ,и получаем, что на промежутке
(-бесконечность; -6) л.ч неравенства больше 0,
таким образом решением неравенства будет
m Є (-бесконечность; -6)обьединение(6;+бесконечность)
Здравствуйте!
Это очень просто.
Сначала переведем с смешанную дробь:
Целая часть, т.е. та, которая стоит перед запятой, слева (1,...) будет в целой части (логично, правда?).
Теперь узнаем как быть с цифрами после запятой (...,8). Это будет числитель. Знаменатель будет всегда 10 у десятичной дроби с 1 цифрой после запятой, 100- 2 цифры после запятой, 1000- 3 цифры и так далее. У нас 1 цифра, будет знаменатель 10.
Получили дробь 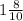
Переведем её в неправильную дробь. Для этого умножим целую часть (1) и знаменталь (10), получаем 10. Прибавляем числитель (8)- 18. Это новый числитель. Знаменталь не меняем, целая часть пропадает.
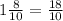
Это неправильная дробь, при возможности сокращаем: