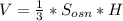
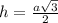
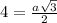
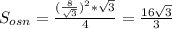
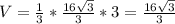
8
Объяснение:
Сложим два равенства, получим уравнение:
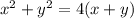
Раскроем скобки справа, перенесем влево и дополним до полных квадратов относительно х и у:
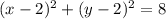
Выражаем x через y:
(вообще, правильнее было бы рассмотреть два случая: когда перед корнем стоит знак плюс, что мы и делаем, и когда перед ним стоит знак минус, но нас интересует максимальное значение, логичнее было бы рассмотреть только положительное значение)
Наша целевая функция, в которой будем находить максимум, имеет вид:
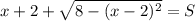, где S - сумма решений системы уравнений.
Найдем производную по х, приравняем к нулю эту функцию
Получим
Таким образом, мы сможем найти y: y₁ = 4; y₂ = 4
Стало быть, только в точке (4;4) достигается этот максимум суммы, которая равна 4+4 = 8
I (17y-y^2)+(-17x-xy)=y(17+y)-x(17+y)=(17+y)(y-x)
II 7a(3a+1)-15(3a+1)=(3a+1)(7a-15)