y = f(x)
Сначала осознаем как должен выглядеть график (рис. 1):
Рисуем прямые x = -5 и x = 6, график не должен выходить за эти прямые (обозначили область определения).Рисуем прямые y = -4 и y = 3, график не должен выходить за эти прямые (обозначили множество значений).На оси Ox отмечаем интервал (1;4), график функции должен проходить через ось Ox в этом интервале (обозначили промежуток нулевого значения).Теперь построим график функции (рис. 2):
Для простоты построим график ломанной (она непрерывна и просто изображается).
Функция убывает на всей области определения, поэтому для самого меньшего х из области определения , должно быть самое наибольшее y из множества значений (потом это значение уже не реализуется т.к. функция убывает, тогда множество значений будет другим). Итог: вершина ломанной в точке (-5;3).Пусть следующая вершина в точке (0;2).Ноль функции, он же пусть будет и вершиной ломанной, в точке (3;0) т.к. 3 ∈ (1;4).Последняя вершина в точке (6;-4), y= -4 для нужного множества значений.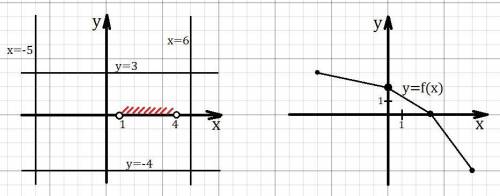
1) Находим производную функции
y'=(x^4-8x³+10x²+1)'=4x³-24x²+20x
2)Находим точки, в которых производная равна нулю:
4x³-24x²+20x=0
4x(x²-6x+5)=0
4x(x-1)(x-5)=0
x₁=0
x₂=1
x₃=5
Из полученных значений нам надо оставить лишь те, которые принадлежат заданному промежутку.
1) ОТРЕЗОК [-2;3]
0∈[-2;3] и 1∈[-2;3], a 5∉[-2;3] Значит находим значения функции в полученных стационарных точках из промежутка и на концах промежутка:
у(0)=0^4-8*0³+10*0²+1=1
у(1)=1^4-8*1³+10*1²+1=1-8+10+1=4
у(-2)=(-2)^4-8(-2)³+10(-2)²+1=4+64+40+1=109 наибольшее значение
у(3)=3^4-8*3³+10*3²+1=81-216+90+1=-44 наименьшее значение
ответ: у наим = -44; у наиб=109
2) ОТРЕЗОК [-1;7]
0∈[-1;7],1∈[-1;7], 5∈[-1;7]
у(0)=0^4-8*0³+10*0²+1=1
у(1)=1^4-8*1³+10*1²+1=1-8+10+1=4
у(5)=5^4-8*5³+10*5²+1=625-1000+250+1=-124 наименьшее значение
y(-1)= (-1)^4-8*(-1)³+10*(-1)²+1=1+8+10+1=20 наибольшее значение
ответ: у наим=-124; у наиб=20